
【题目】已知函数f(x)= ![]() .
.
(1)求f(f( ![]() ));
));
(2)若x0满足f(f(x0))=x0 , 且f(x0)≠x0 , 则称x0为f(x)的二阶不动点,求函数f(x)的二阶不动点的个数.
【答案】
(1)解:∵f(x)= ![]() .
.
∴f( ![]() ))=ln
))=ln ![]() =
= ![]() ,
,
∴f(f( ![]() ))=f(
))=f( ![]() )=2﹣2×
)=2﹣2× ![]() =1
=1
(2)解:函数f(x)= ![]() .x∈[0,
.x∈[0, ![]() ),f(x)=2﹣2x∈(1,2],
),f(x)=2﹣2x∈(1,2],
x∈[ ![]() ,1),f(x)=2﹣2x∈(0,1],
,1),f(x)=2﹣2x∈(0,1],
x∈[1,e],f(x)=lnx∈(0,1),
∴f(f(x))= 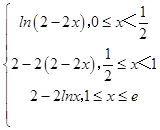 ,
,
若x0满足f(f(x0))=x0,且f(x0)≠x0,则称x0为f(x)的二阶不动点,
所以:x0∈[0, ![]() ),ln(2﹣2x0)=x0,由y=ln(2﹣x0),y=x0,图象可知:
),ln(2﹣2x0)=x0,由y=ln(2﹣x0),y=x0,图象可知:
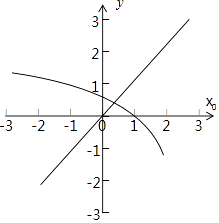
存在满足题意的不动点.
x0∈[ ![]() ,1),﹣2+4x0=x0,解得x0=
,1),﹣2+4x0=x0,解得x0= ![]() ,满足题意.
,满足题意.
x0∈[1,e],2﹣2lnx0=x0,即2﹣x0=2lnx0,由y=2﹣x0,y=2lnx0,图象可知:

存在满足题意的不动点.
函数f(x)的二阶不动点的个数为:3个
【解析】(1)利用分段函数,逐步求解函数值即可.(2)利用分段函数求出f(f(x0))的解析式,然后通过求解方程得到函数f(x)的二阶不动点的个数.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=1,AB=2. 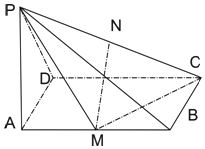
(1)求证:MN∥平面PAD;
(2)求证:平面PMC⊥平面PCD;
(3)求点D到平面PMC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示,则关于f(x)的说法正确的是( )
)的部分图象如图所示,则关于f(x)的说法正确的是( ) 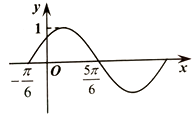
A.对称轴方程是x= ![]() +2kπ(k∈Z)
+2kπ(k∈Z)
B.φ=﹣ ![]()
C.最小正周期为π
D.在区间( ![]() ,
, ![]() )上单调递减
)上单调递减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图正方体ABCD﹣A1B1C1D1 , M,N分别为A1D1和AA1的中点,则下列说法中正确的个数为( ) 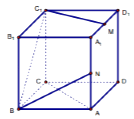
①C1M∥AC;
②BD1⊥AC;
③BC1与AC的所成角为60°;
④B1A1、C1M、BN三条直线交于一点.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,若 ![]() (acosB+bcosA)=2csinC,a+b=4,且△ABC的面积的最大值为
(acosB+bcosA)=2csinC,a+b=4,且△ABC的面积的最大值为 ![]() ,则此时△ABC的形状为( )
,则此时△ABC的形状为( )
A.锐角三角形
B.直线三角形
C.等腰三角形
D.正三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3x , g(x)=|x+a|﹣3,其中a∈R. (Ⅰ)若函数h(x)=f[g(x)]的图象关于直线x=2对称,求a的值;
(Ⅱ)给出函数y=g[f(x)]的零点个数,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com