
分析 根据直线2x+y+4=0方程求出它与x轴、y轴交点A、B的坐标,从而得到该圆以AB中点C(-1,-2)为圆心,半径长为$\frac{1}{2}$|AB|=$\sqrt{5}$,最后根据圆的标准方程列式即可得到所求圆的方程.
解答 解:∵对直线2x+y+4=0,令x=0,得y=-4;令y=0,得x=-2
∴直线2x+y+4=0交x轴于A(-2,0),交y轴于B(0,-4)
∵所求的圆以AB为直径
∴该圆以AB中点C(-1,-2)为圆心,半径长为$\frac{1}{2}$|AB|=$\sqrt{5}$
∴圆C的方程为(x+1)2+(y+2)2=5,
故答案为:(x+1)2+(y+2)2=5.
点评 本题给出已知直线,求以直线被两坐标轴截得线段为直径的圆方程,着重考查了中点坐标公式、圆的标准方程和两点间的距离公式等知识,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
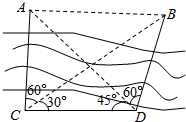 如图,A、B两点都在河的对岸(不可到达),测量者在河岸边选定两点C、D,测得CD=40m,并且在C、D两点分别测得∠ACB=60°,∠ADB=60°∠BCD=30°,∠ADC=45°,求河的对岸的两点A、B间的距离.
如图,A、B两点都在河的对岸(不可到达),测量者在河岸边选定两点C、D,测得CD=40m,并且在C、D两点分别测得∠ACB=60°,∠ADB=60°∠BCD=30°,∠ADC=45°,求河的对岸的两点A、B间的距离.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com