
已知点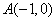 ,
,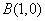 ,
,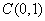 ,直线
,直线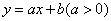 将
将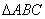 分割为面积相等的两部分,则
分割为面积相等的两部分,则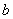 的取值范围是( )
的取值范围是( )
(A) (B)
(B)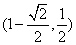 (C)
(C)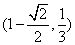 (D)
(D)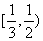
B
解:分两种情况:
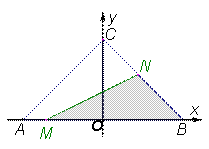
①直线y = ax +b与AC、BC相交时,如图所示,设MC = m, NC = n,
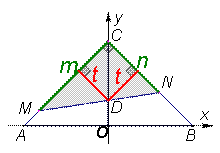 由条件知S△MNC =
由条件知S△MNC = 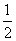 ⇒ mn = 1
⇒ mn = 1
显然0 < n ≤ 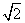 ⇒ m =
⇒ m = 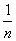 ≥
≥ 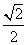 又知0 < m ≤
又知0 < m ≤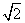 , m ≠ n
, m ≠ n
所以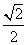 ≤ m ≤
≤ m ≤ 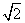 且m ≠ 1
且m ≠ 1
D到AC、BC的距离为t, 则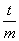 +
+ 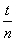 =
= 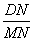 +
+ 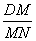 = 1
= 1
⇒ t = 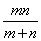 ⇒
⇒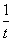 = m +
= m + 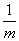
f (m ) = m + 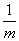 (
(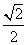 ≤ m ≤
≤ m ≤ 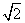 且m ≠ 1)的值域为(2,
且m ≠ 1)的值域为(2, 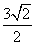 ] ⇒ 2 <
] ⇒ 2 < 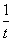 ≤
≤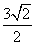 ⇒
⇒ 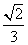 ≤ t <
≤ t < 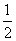
 因为b =1 CD =1
因为b =1 CD =1 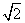 t ,所以1
t ,所以1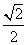 < b ≤
< b ≤ 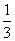
②:直线y = ax +b与AB、BC相交时,如图所示,
易求得xM =  , yN =
, yN = 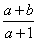 ,由条件知(1+
,由条件知(1+  )
) 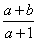 = 1
= 1
⇒ 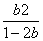 = a
= a
M在线段OA上⇒0<  <1 ⇒0 < a < b
<1 ⇒0 < a < b
N在线段BC上⇒0< 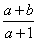 <1 ⇒b < 1
<1 ⇒b < 1
解不等式:0 < 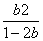 < b得
< b得 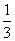 < b <
< b < 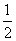
综上:1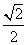 < b <
< b < 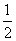


科目:高中数学 来源: 题型:
已知定义在R上的函数f(x)和数列{an}满足下列条件:
a1=a,an=f(aa-1)(n=2,3,4,…),a2≠a1,f(an)-f(an-1)=k(an-an-1)(n=2,3,4,…),其中a为常数,k为非零常
数.
(Ⅰ)令bn=aa+1-an(n∈N*),证明数列{bn}是等比数列;
(Ⅱ)求数列{an}的通项公式 ;
;
(Ⅲ)当|k|<1时,求
查看答案和解析>>
科目:高中数学 来源: 题型:
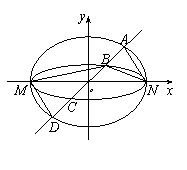
如图,已知椭圆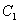 与
与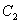 的中心在坐标原点
的中心在坐标原点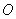 ,长轴均为
,长轴均为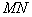 且在
且在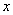 轴上,短轴长分别为
轴上,短轴长分别为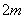 ,
,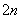
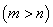 ,过原点且不与
,过原点且不与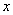 轴重合的直线
轴重合的直线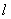 与
与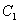 ,
,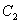 的四个交点按纵坐标从大到小依次为
的四个交点按纵坐标从大到小依次为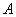 ,
,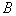 ,
, ,
,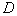 。记
。记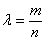 ,
,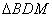 和
和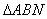 的面积分别为
的面积分别为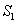 和
和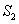 。
。
(I)当直线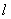 与
与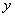 轴重合时,若
轴重合时,若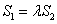 ,求
,求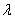 的值;
的值;
(II)当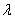 变化时,是否存在与坐标轴不重合的直线
变化时,是否存在与坐标轴不重合的直线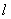 ,使得
,使得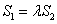 ?并说明理由。
?并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com