
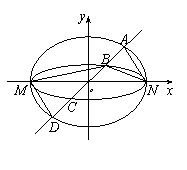
如图,已知椭圆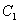 与
与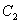 的中心在坐标原点
的中心在坐标原点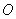 ,长轴均为
,长轴均为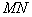 且在
且在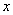 轴上,短轴长分别为
轴上,短轴长分别为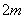 ,
,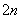
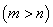 ,过原点且不与
,过原点且不与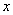 轴重合的直线
轴重合的直线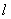 与
与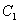 ,
,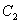 的四个交点按纵坐标从大到小依次为
的四个交点按纵坐标从大到小依次为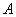 ,
,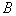 ,
, ,
,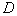 。记
。记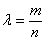 ,
,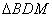 和
和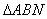 的面积分别为
的面积分别为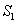 和
和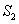 。
。
(I)当直线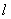 与
与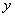 轴重合时,若
轴重合时,若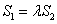 ,求
,求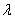 的值;
的值;
(II)当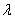 变化时,是否存在与坐标轴不重合的直线
变化时,是否存在与坐标轴不重合的直线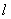 ,使得
,使得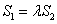 ?并说明理由。
?并说明理由。
【解析】(Ⅰ)依题意可设椭圆 和
和 的方程分别为
的方程分别为
 :
: ,
, :
: . 其中
. 其中 ,
,
解法1:如图1,若直线 与
与 轴重合,即直线
轴重合,即直线 的方程为
的方程为 ,则
,则
 ,
, ,所以
,所以 .
.
在C1和C2的方程中分别令 ,可得
,可得 ,
, ,
, ,
,
于是 .
.
若 ,则
,则 ,化简得
,化简得 . 由
. 由 ,可解得
,可解得 .
.
故当直线 与
与 轴重合时,若
轴重合时,若 ,则
,则 .
.
解法2:如图1,若直线 与
与 轴重合,则
轴重合,则
 ,
, ;
;
 ,
, .
.


所以 .
.
若 ,则
,则 ,化简得
,化简得 . 由
. 由 ,可解得
,可解得 .
.
故当直线 与
与 轴重合时,若
轴重合时,若 ,则
,则 .
.
(Ⅱ)解法1:如图2,若存在与坐标轴不重合的直线l,使得 . 根据对称性,
. 根据对称性,
不妨设直线 :
: ,
,
点 ,
, 到直线
到直线 的距离分别为
的距离分别为 ,
, ,则
,则
因为 ,
, ,所以
,所以 .
.
又 ,
, ,所以
,所以 ,即
,即 .
.
由对称性可知 ,所以
,所以 ,
,
 ,于是
,于是
 . ①
. ①
将 的方程分别与C1,C2的方程联立,可求得
的方程分别与C1,C2的方程联立,可求得
 ,
, .
.
根据对称性可知 ,
, ,于是
,于是
 . ②
. ②
从而由①和②式可得
 . ③
. ③
令 ,则由
,则由 ,可得
,可得 ,于是由③可解得
,于是由③可解得 .
.
因为 ,所以
,所以 . 于是③式关于
. 于是③式关于 有解,当且仅当
有解,当且仅当 ,
,
等价于 . 由
. 由 ,可解得
,可解得 ,
,
即 ,由
,由 ,解得
,解得 ,所以
,所以
当 时,不存在与坐标轴不重合的直线l,使得
时,不存在与坐标轴不重合的直线l,使得 ;
;
当 时,存在与坐标轴不重合的直线l使得
时,存在与坐标轴不重合的直线l使得 .
.


科目:高中数学 来源: 题型:
等比数列{an}中,a1=512,公比q=- ,用Ⅱn
,用Ⅱn 表示它的前n项之积:Ⅱn=a1·a2…an,则Ⅱ1,Ⅱ2…中最大的是 ( )
表示它的前n项之积:Ⅱn=a1·a2…an,则Ⅱ1,Ⅱ2…中最大的是 ( )
A.Ⅱ11 B.Ⅱ10 C.Ⅱ9 D.Ⅱ8
查看答案和解析>>
科目:高中数学 来源: 题型:
设数列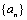 是首项大于零的等比数列,则“
是首项大于零的等比数列,则“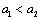 ”是“数列
”是“数列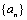 是递增数列”的( )
是递增数列”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com