
分析 (1)根据真数大于0,可得函数的定义域,根据对数的运算性质,可得f(-x)=-f(x)得:f(x)为奇函数;
(2)由f(x)的值域为(-∞,1)求出相应的自变量的取值范围,可得a与t的值.
解答 解:(1)由$\frac{1-x}{1+x}$>0得:x∈(-1,1),
故函数f(x)的定义域D=(-1,1);
由函数f(x)的定义域关于原点对称,
且f(-x)=loga$\frac{1+x}{1-x}$=-loga$\frac{1-x}{1+x}$=-f(x)得:f(x)为奇函数;
(2)∵0<a<1,
故f(x)的值域为(-∞,1)时,$\frac{1-x}{1+x}$>a,
即$\frac{(a+1)x+(a-1)}{x+1}<0$,
解得:x∈(-1,$\frac{1-a}{a+1}$),
∴t=-1,a=$\frac{1-a}{a+1}$,
解得:a=$\frac{-1+\sqrt{2}}{2}$,或a=$\frac{-1-\sqrt{2}}{2}$(舍去),
综上:a=$\frac{-1+\sqrt{2}}{2}$,t=-1
点评 本题考查的知识点是对数函数的图象和性质,熟练掌握对数函数的图象和性质,是解答的关键.


科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+2y+1=0 | B. | 2x+2y-1=0 | C. | 2x-2y-1=0 | D. | 2x-2y-3=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
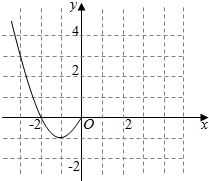 已知函数f(x)是定义在R上的偶函数,现已画出函数f(x)在y轴左侧的图象,如图所示,请根据图象:
已知函数f(x)是定义在R上的偶函数,现已画出函数f(x)在y轴左侧的图象,如图所示,请根据图象:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| A组 | B组 | C组 | |
| 疫苗有效 | 903 | x | y |
| 疫苗无效 | 197 | 90 | z |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
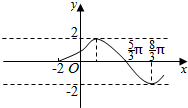
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com