Question

3．函数y=$\left\{\begin{array}{l}{kx+1（-2≤x≤0）}\\{2sin（ωx+φ）（ω＞0，0＜x≤\frac{8π}{3}）}\end{array}\right.$的图象如图，则k=$\frac{1}{2}$，ω=$\frac{1}{2}$，φ=$\frac{π}{6}$．

Answer 1

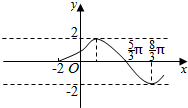
分析 由直线y=kx+1过点（-2，0）得k=$\frac{1}{2}$；可确定$\frac{T}{4}$=$\frac{8π}{3}$-$\frac{5π}{3}$=π，从而确定ω=$\frac{1}{2}$，再代入点求φ即可．

解答 解：∵直线y=kx+1过点（-2，0），
∴k=$\frac{1}{2}$；
∵$\frac{T}{4}$=$\frac{8π}{3}$-$\frac{5π}{3}$=π，
∴T=4π，
∴ω=$\frac{2π}{4π}$=$\frac{1}{2}$，
（$\frac{8π}{3}$，-2）代入y=2sin（$\frac{1}{2}$x+φ）得，
sin（$\frac{4π}{3}$+φ）=-1，
解得，φ=$\frac{π}{6}$；
故答案为：$\frac{1}{2}$，$\frac{1}{2}$，$\frac{π}{6}$．

点评 本题考查了分段函数及数形结合的思想应用．