
【题目】某校为了解高三年级不同性别的学生对取消艺术课的态度(支持或反对),进行了如下的调查研究,全年级共有1350人,男女生比例为![]() ,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为
,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为![]() ,通过对被抽取学生的问卷调查,得到如下
,通过对被抽取学生的问卷调查,得到如下![]() 列联表:
列联表:
支持 | 反对 | 总计 | |
男生 | 30 | ||
女生 | 25 | ||
总计 |
(1)完成列联表,并判断能否有![]() 的把握认为态度与性别有关?
的把握认为态度与性别有关?
(2)若某班有6名男生被抽到,其中2人支持,4人反对;有4名女生被抽到,其中2人支持,2人反对,现从这10人中随机抽取一男一女进一步调查原因.求其中恰有一人支持一人反对的概率.
参考公式及临界值表:![]()
| 0.10 | 0.050 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
【答案】(1)列联表见解析,没有(2)![]()
【解析】
(1)根据题意,分别算出抽取样本中男生和女生的人数,便可完成列联表;求出![]() ,与临界值比较,即可得出能否有
,与临界值比较,即可得出能否有![]() 的把握认为态度与性别有关;
的把握认为态度与性别有关;
(2)列举出基本事件,确定基本事件的个数,根据古典概型的概率公式,可得结论.
(1)由题意可知,全年级共有1350人,每人被抽到的概率均为![]() ,
,
所以抽取样本容量为:![]() ,
,
其中男生人数为:![]() ,女生人数为:
,女生人数为:![]() ,
,
则列联表如下:
支持 | 反对 | 总计 | |
男生 | 30 | 50 | 80 |
女生 | 45 | 25 | 70 |
总计 | 75 | 75 | 150 |
计算得![]() ,
,
所以没有![]() 的把握认为态度与性别有关,
的把握认为态度与性别有关,
(2)记6名男生为![]() ,其中
,其中![]() 为支持,
为支持,![]() 为反对,
为反对,
记4名女生为![]() ,其中
,其中![]() 为支持,
为支持,![]() 为反对,
为反对,
随机抽取一男一女所有可能的情况有24种,分别为:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
其中恰有一人支持一人反对的可能情况有12种,所以概率为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的发展理念,某城区对辖区内![]() ,
,![]() ,
,![]() 三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到80分及其以上的单位被称为“星级”环保单位,未达到80分的单位被称为“非星级”环保单位.现通过分层抽样的方法获得了这三类行业的20个单位,其考评分数如下:
三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到80分及其以上的单位被称为“星级”环保单位,未达到80分的单位被称为“非星级”环保单位.现通过分层抽样的方法获得了这三类行业的20个单位,其考评分数如下:
![]() 类行业:85,82,77,78,83,87;
类行业:85,82,77,78,83,87;
![]() 类行业:76,67,80,85,79,81;
类行业:76,67,80,85,79,81;
![]() 类行业:87,89,76,86,75,84,90,82.
类行业:87,89,76,86,75,84,90,82.
(Ⅰ)计算该城区这三类行业中每类行业的单位个数;
(Ⅱ)若从抽取的![]() 类行业这6个单位中,再随机选取3个单位进行某项调查,求选出的这3个单位中既有“星级”环保单位,又有“非星级”环保单位的概率.
类行业这6个单位中,再随机选取3个单位进行某项调查,求选出的这3个单位中既有“星级”环保单位,又有“非星级”环保单位的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:x2≤5x-4,q:x2-(a+2)x+2a≤0.
(1)若p是真命题,求对应x的取值范围;
(2)若p是q的必要不充分条件,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公差为正数的等差数列,数列
是公差为正数的等差数列,数列![]() 为等比数列,且
为等比数列,且![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)设数列![]() 是由所有
是由所有![]() 的项,且
的项,且![]() 的项组成的数列,且原项数先后顺序保持不变,求数列
的项组成的数列,且原项数先后顺序保持不变,求数列![]() 的前2019项的和
的前2019项的和![]() ;
;
(3)对任意给定的![]() 是否存在
是否存在![]() 使
使![]() 成等差数列?若存在,用
成等差数列?若存在,用![]() 分别表示
分别表示![]() 和
和![]() (只要写出一组即可);若不存在,请说明理由.
(只要写出一组即可);若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年某地区初中升学体育考试规定:考生必须参加长跑、掷实心球、1分钟跳绳三项测试.某学校在九年级上学期开始,就为掌握全年级学生1分钟跳绳情况,抽取了100名学生进行测试,得到下面的频率分布直方图.
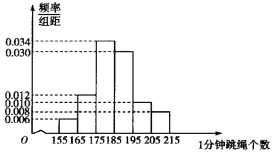
(Ⅰ)规定学生1分钟跳绳个数大于等于185为优秀.若在抽取的100名学生中,女生共有50人,男生1分钟跳绳个数大于等于185的有28人.根据已知条件完成下面的![]() 列联表,并根据这100名学生的测试成绩,判断能否有99%的把握认为学生1分钟跳绳成绩是否优秀与性别有关.
列联表,并根据这100名学生的测试成绩,判断能否有99%的把握认为学生1分钟跳绳成绩是否优秀与性别有关.
1分钟跳绳成绩 | 优秀 | 不优秀 | 合计 |
男生人数 | 28 | ||
女生人数 | 100 | ||
合计 | 100 |
(Ⅱ)根据往年经验,该校九年级学生经过训练,正式测试时每人1分钟跳绳个数都有明显进步.假设正式测试时每人1分钟跳绳个数都比九年级上学期开始时增加10个,全年级恰有2000名学生,若所有学生的1分钟跳绳个数![]() 服从正态分布
服从正态分布![]() ,用样本数据的平均值和标准差估计
,用样本数据的平均值和标准差估计![]() 和
和![]() ,各组数据用中点值代替),估计正式测试时1分钟跳绳个数大于183的人数(结果四舍五入到整数
,各组数据用中点值代替),估计正式测试时1分钟跳绳个数大于183的人数(结果四舍五入到整数
附: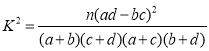 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]()
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() ,过点
,过点![]() 的直线
的直线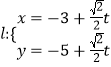 (
(![]() 为参数)与曲线
为参数)与曲线![]() 相交于点
相交于点![]() ,
,![]() 两点.
两点.
(1)求曲线![]() 的平面直角坐标系方程和直线
的平面直角坐标系方程和直线![]() 的普通方程;
的普通方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856331)
甲、乙两家快餐店对某日7个时段的光顾的客人人数进行统计并绘制茎叶图如下图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.
(Ⅰ)求a,b的值,并计算乙数据的方差;
(Ⅱ)现从乙数据中不大于16的数据中随机抽取两个,求至少有一个数据小于10的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的质量指标值.由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[55,65),[65,75),[75,85]内的频率之比为4∶2∶1.
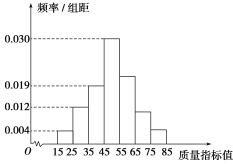
(1)求这些产品质量指标值落在区间[75,85]内的概率;
(2)若将频率视为概率,从该企业生产的这种产品中随机抽取3件,记这3件产品中质量指标值位于区间[45,75)内的产品件数为X,求X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了工厂技术改造后某种型号设备的使用年限x和所支出的维修费y(万元)的几组对照数据:
x(年) | 2 | 3 | 4 | 5 | 6 |
y(万元) | 1 | 2.5 | 3 | 4 | 4.5 |
(1)若知道y对x呈线性相关关系,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(2)已知该工厂技术改造前该型号设备使用10年的维修费用为9万元,试根据(1)求出的线性回归方程,预测该型号设备技术改造后,使用10年的维修费用能否比技术改造前降低?参考公式: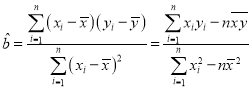 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com