
【题目】已知底面为边长为![]() 的正方形,侧棱长为
的正方形,侧棱长为![]() 的直四棱柱
的直四棱柱![]() 中,
中,![]() 是上底面
是上底面![]() 上的动点.给出以下四个结论中,正确的个数是( )
上的动点.给出以下四个结论中,正确的个数是( )
①与点![]() 距离为
距离为![]() 的点
的点![]() 形成一条曲线,则该曲线的长度是
形成一条曲线,则该曲线的长度是![]() ;
;
②若![]() 面
面![]() ,则
,则![]() 与面
与面![]() 所成角的正切值取值范围是
所成角的正切值取值范围是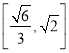 ;
;
③若![]() ,则
,则![]() 在该四棱柱六个面上的正投影长度之和的最大值为
在该四棱柱六个面上的正投影长度之和的最大值为![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
①与点![]() 距离为
距离为![]() 的点
的点![]() 形成以
形成以![]() 为圆心,半径为
为圆心,半径为![]() 的
的![]() 圆弧
圆弧![]() ,利用弧长公式,可得结论;②当
,利用弧长公式,可得结论;②当![]() 在
在![]() (或
(或![]() 时,
时,![]() 与面
与面![]() 所成角
所成角![]() (或
(或![]() 的正切值为
的正切值为![]() 最小,当
最小,当![]() 在
在![]() 时,
时,![]() 与面
与面![]() 所成角
所成角![]() 的正切值为
的正切值为![]() 最大,可得正切值取值范围是
最大,可得正切值取值范围是![]() ;③设
;③设![]() ,
,![]() ,
,![]() ,则
,则![]() ,即
,即![]() ,可得
,可得![]() 在前后、左右、上下面上的正投影长,即可求出六个面上的正投影长度之和.
在前后、左右、上下面上的正投影长,即可求出六个面上的正投影长度之和.
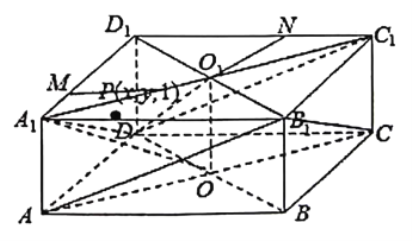
如图:
①错误, 因为![]() ,与点
,与点![]() 距离为
距离为![]() 的点
的点![]() 形成以
形成以![]() 为圆心,半径为
为圆心,半径为![]() 的
的![]() 圆弧
圆弧![]() ,长度为
,长度为![]() ;
;
②正确,因为面![]() 面
面![]() ,所以点
,所以点![]() 必须在面对角线
必须在面对角线![]() 上运动,当
上运动,当![]() 在
在![]() (或
(或![]() )时,
)时,![]() 与面
与面![]() 所成角
所成角![]() (或
(或![]() )的正切值为
)的正切值为![]() 最小(
最小(![]() 为下底面面对角线的交点),当
为下底面面对角线的交点),当![]() 在
在![]() 时,
时,![]() 与面
与面![]() 所成角
所成角![]() 的正切值为
的正切值为![]() 最大,所以正切值取值范围是
最大,所以正切值取值范围是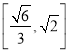 ;
;
③正确,设![]() ,则
,则![]() ,即
,即![]() ,
,![]() 在前后、左右、上下面上的正投影长分别为
在前后、左右、上下面上的正投影长分别为![]() ,
,![]() ,
,![]() ,所以六个面上的正投影长度之
,所以六个面上的正投影长度之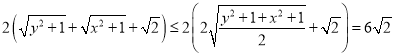 ,当且仅当
,当且仅当![]() 在
在![]() 时取等号.
时取等号.
故选:![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为![]() ,(t为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C1:ρ=2cosθ,
,(t为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C1:ρ=2cosθ,![]() .
.
(1)求C1与C2交点的直角坐标;
(2)若直线l与曲线C1,C2分别相交于异于原点的点M,N,求|MN|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今有6个人组成的旅游团,包括4个大人,2个小孩,去庐山旅游,准备同时乘缆车观光,现有三辆不同的缆车可供选择,每辆缆车最多可乘3人,为了安全起见,小孩乘缆车必须要大人陪同,则不同的乘车方式有_____种.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建极坐标系,直线
轴的非负半轴为极轴建极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(Ⅰ)求![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)射线![]() 与圆C的交点为
与圆C的交点为![]() 与直线
与直线![]() 的交点为
的交点为![]() ,求
,求![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设二次函数![]() .
.
(1)若![]() ,求
,求![]() 的解析式;
的解析式;
(2)当![]() ,
,![]() 时,对任意的
时,对任意的![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() 在两个不同零点
在两个不同零点![]() ,将关于
,将关于![]() 的不等式
的不等式![]() 的解集记为
的解集记为![]() .已知函数
.已知函数![]() 的最小值为
的最小值为![]() ,且函数
,且函数![]() 在
在![]() 上不存在最小值,求实数
上不存在最小值,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂![]() ,
,![]() 两条相互独立的生产线生产同款产品,在产量一样的情况下通过日常监控得知
两条相互独立的生产线生产同款产品,在产量一样的情况下通过日常监控得知![]() ,
,![]() 生产线生产的产品为合格品的概率分别为
生产线生产的产品为合格品的概率分别为![]() 和
和![]() .
.
(1)从![]() ,
,![]() 生产线上各抽检一件产品,若使得至少有一件合格的概率不低于
生产线上各抽检一件产品,若使得至少有一件合格的概率不低于![]() ,求
,求![]() 的最小值
的最小值![]() .
.
(2)假设不合格的产品均可进行返工修复为合格品,以(1)中确定的![]() 作为
作为![]() 的值.
的值.
①已知![]() ,
,![]() 生产线的不合格产品返工后每件产品可分别挽回损失
生产线的不合格产品返工后每件产品可分别挽回损失![]() 元和
元和![]() 元。若从两条生产线上各随机抽检
元。若从两条生产线上各随机抽检![]() 件产品,以挽回损失的平均数为判断依据,估计哪条生产线挽回的损失较多?
件产品,以挽回损失的平均数为判断依据,估计哪条生产线挽回的损失较多?
②若最终的合格品(包括返工修复后的合格品)按照一、二、三等级分类后,每件分别获利![]() 元、
元、![]() 元、
元、![]() 元,现从
元,现从![]() ,
,![]() 生产线的最终合格品中各随机抽取
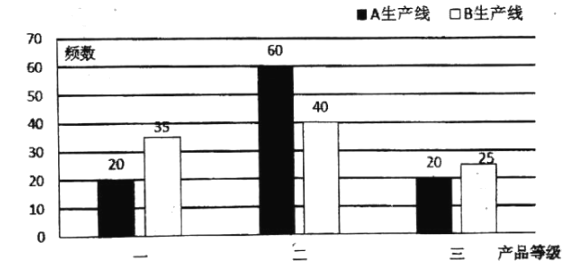
生产线的最终合格品中各随机抽取![]() 件进行检测,结果统计如下图;用样本的频率分布估计总体分布,记该工厂生产一件产品的利润为
件进行检测,结果统计如下图;用样本的频率分布估计总体分布,记该工厂生产一件产品的利润为![]() ,求
,求![]() 的分布列并估算该厂产量
的分布列并估算该厂产量![]() 件时利润的期望值.
件时利润的期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是国家统计局公布的2013-2018年入境游客(单位:万人次)的变化情况,则下列结论错误的是( )

A.2014年我国入境游客万人次最少
B.后4年我国入境游客万人次呈逐渐增加趋势
C.这6年我国入境游客万人次的中位数大于13340万人次
D.前3年我国入境游客万人次数据的方差小于后3年我国入境游客万人次数据的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的方程为
的方程为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,直线
,直线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,与曲线
,与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,
,![]() ,
,![]() 成等比数列,求直线
成等比数列,求直线![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着共享单车的成功运营,更多的共享产品逐步走入大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷.广元某景点设有共享电动车租车点,共享电动车的收费标准是每小时2元(不足1小时的部分按1小时计算).甲、乙两人各租一辆电动车,若甲、乙不超过一小时还车的概率分别为![]() ,
,![]() ;一小时以上且不超过两小时还车的概率分别为
;一小时以上且不超过两小时还车的概率分别为![]() ,
,![]() ;两人租车时间都不会超过三小时.
;两人租车时间都不会超过三小时.
(1)求甲、乙两人所付租车费用相同的概率;
(2)求甲、乙两人所付的租车费用之和大于或等于8的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com