
分析 由0<x<1,可得x<$\frac{1}{x}$,x+$\frac{1}{x}$>0.利用乘法公式、根式的运算性质化简即可得出.
解答 解:∵0<x<1,∴x<$\frac{1}{x}$,x+$\frac{1}{x}$>0.
∴$\sqrt{(x-\frac{1}{x})^{2}+4}$-$\sqrt{(x+\frac{1}{x})^{2}-4}$=$\sqrt{(x+\frac{1}{x})^{2}}$-$\sqrt{(x-\frac{1}{x})^{2}}$=x+$\frac{1}{x}$-$(\frac{1}{x}-x)$=2x,
故答案为:2x.
点评 本题考查了不等式的性质、乘法公式、根式的运算性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
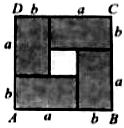 如图所示,设小矩形的长、宽各为a,b,现把四个同样的矩形拼接成正方形后,分析其中阴影部分矩形面积之和与正方形面积之间的关系,并用不等式表达出来.
如图所示,设小矩形的长、宽各为a,b,现把四个同样的矩形拼接成正方形后,分析其中阴影部分矩形面积之和与正方形面积之间的关系,并用不等式表达出来.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是三个向量的数量积 | B. | 是与$\overrightarrow{a}$共线的向量 | ||
| C. | 是与$\overrightarrow{c}$共线的向量 | D. | 无意义 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | a>b>c | C. | b>a>c | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\sqrt{3}$ | B. | ±$\frac{\sqrt{3}}{3}$ | C. | ±1 | D. | ±$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com