
| A. | 0 | B. | -80x2 | C. | 80x2 | D. | 160x2 |
分析 由于二项式展开式中各项的系数的和为2,故可以令x=1,建立a的方程,解出a的值,然后写出(2x-$\frac{1}{x}$)5 的展开式的通项,进一步求得展开式中含x2项.
解答 解:令x=1,则有1+a=2,得a=1,故二项式为(x+$\frac{1}{x}$)(2x-$\frac{1}{x}$)5 ,
(2x-$\frac{1}{x}$)5 的展开式的通项为${T}_{r+1}={C}_{5}^{r}(2x)^{5-r}(-\frac{1}{x})^{r}$=$(-1)^{r}{2}^{5-r}{C}_{5}^{r}{x}^{5-2r}$,
则展开式(x+$\frac{1}{x}$)(2x-$\frac{1}{x}$)5 中含x2项为$[(-1)^{2}{2}^{3}{C}_{5}^{2}+(-1)^{1}{2}^{4}{C}_{5}^{1}]{x}^{2}=0$.
故选:A.
点评 本题考查二项式系数的性质,解题关键是掌握二项式系数的公式,以及根据二项式的形式判断出含x2项,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC,EA⊥EB.
如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC,EA⊥EB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
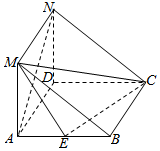 如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ABCD是菱形,∠DAB=60°,AD=2,侧面ADNM是矩形,AM=1.E是AB的中点.
如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ABCD是菱形,∠DAB=60°,AD=2,侧面ADNM是矩形,AM=1.E是AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com