
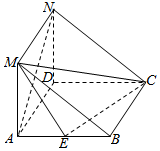
 如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ABCD是菱形,∠DAB=60°,AD=2,侧面ADNM是矩形,AM=1.E是AB的中点.
如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ABCD是菱形,∠DAB=60°,AD=2,侧面ADNM是矩形,AM=1.E是AB的中点.分析 (1)连结MD,设AN∩MD=G,取MC中点F,连结EF,GF,则利用中位线定理和平行公理可得四边形AEFG是平行四边形,得出AN∥EF,故而AN∥平面MEC;
(2)以△BCM为底面,则AM为棱锥的高,根据菱形的性质求出△BCE的面积,代入棱锥的体积公式计算.
解答 (1)证明连结MD,设AN∩MD=G,取MC中点F,连结EF,GF,
∵侧面ADNM是矩形,∴G是MD的中点,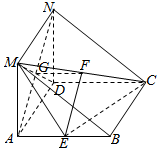
∴GF是△MCD的中位线,
∴GF∥CD,GF=$\frac{1}{2}CD$,
∵侧面ABCD是菱形,E是AB的中点,
∴AE∥CD,AE=$\frac{1}{2}CD$,
∴GF∥AE,GF=AE,
∴四边形AEFG是平行四边形,
∴AG∥EF,即AN∥EF,
又∵AN?平面MEC,EF?平面MEC,
∴AN∥平面MEC.
(2)解:∵侧面ADNM是矩形,∴AM⊥AD,
又∵侧面ADNM⊥侧面ABCD,侧面ADNM∩侧面ABCD=AD,AM?平面ADNM,
∴AM⊥平面ABCD.
∵侧面ABCD是菱形,∠DAB=60°,AD=2,
∴BE=1,∠EBC=120°,BC=2,
∴S△BCE=$\frac{1}{2}×1×2×sin120°$=$\frac{\sqrt{3}}{2}$.
∴VE-BCM=VM-BCE=$\frac{1}{3}{S}_{△BCE}•AM$=$\frac{1}{3}×\frac{\sqrt{3}}{2}×1$=$\frac{\sqrt{3}}{6}$.
点评 本题考查了线面平行的判定,面面垂直的性质,棱锥的体积计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -80x2 | C. | 80x2 | D. | 160x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 高校 | 相关人数 | 抽取人数 |
| A | 54 | x |
| B | 36 | 2 |
| C | 72 | y |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 产品编号 | A1 | A2 | A3 | A4 | A5 |
| 质量指标(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
| 产品编号 | A6 | A7 | A8 | A9 | A10 |
| 质量指标(x,y,z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直三棱柱ABC-A1B1C1中,底面ABC是正三角形,点D是BC的中点,BC=BB1.
如图,在直三棱柱ABC-A1B1C1中,底面ABC是正三角形,点D是BC的中点,BC=BB1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-∞,-1]∪(0,1) | C. | [-1,4] | D. | (-∞,-1]∪[0,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 可去间断点 | B. | 无穷间断点 | C. | 连续点 | D. | 跳跃间断点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com