
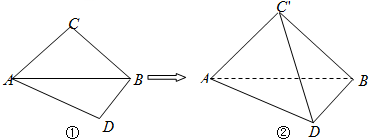
分析 (1)取AB的中点O,连C′O,DO,通过就是证明C′O⊥OD,证明C′O⊥平面ABD,然后证明平面C′AB⊥平面DAB.
(2)以O为原点,AB,OC′所在的直线分别为y,z轴,建立如图空间直角坐标系,
求出平面AC′D的法向量,平面BC′D的法向量,利用向量的数量积求解二面角A-C′D-B的余弦值.
解答 解:(1)取AB的中点O,连C′O,DO,
在RT△ACB,RT△ADB,AB=2,则C′O=DO=1,又,∴C′O2+DO2=C′D2,即C′O⊥OD,…(2分)
又,AB∩OD=O,AB,OD?平面ABD∴C′O⊥平面ABD,…(4分)
又C′O?平面ABC′∴平面C′AB⊥平面DAB…(5分)
(2)以O为原点,AB,OC′所在的直线分别为y,z轴,建立如图空间直角坐标系,
则$A(0,-1,0),B(0,1,0),C′(0,0,1),D(\frac{{\sqrt{3}}}{2},\frac{1}{2},0)$,
∴$\overrightarrow{AC′}=(0,1,1),\overrightarrow{BC′}=(0,-1,1),\overrightarrow{C′D}=(\frac{{\sqrt{3}}}{2},\frac{1}{2},-1)$…(6分)
设平面AC′D的法向量为$\overrightarrow{n_1}=({x_1},{y_1},{z_1})$,则$\left\{\begin{array}{l}\overrightarrow{n_1}⊥\overrightarrow{AC′}\\ \overrightarrow{n_1}⊥\overrightarrow{C′D}\end{array}\right.$,即$\left\{\begin{array}{l}\overrightarrow{n_1}•\overrightarrow{AC′}=0\\ \overrightarrow{n_1}•\overrightarrow{C′D}=0\end{array}\right.$,
$\left\{\begin{array}{l}{y_1}+{z_1}=0\\ \frac{{\sqrt{3}}}{2}{x_1}+\frac{1}{2}{y_1}-{z_1}=0\end{array}\right.$,
令z1=1,则y1=-1,${x_1}=\sqrt{3}$,∴$\overrightarrow{n_1}=(\sqrt{3},-1,1)$…(8分)
设平面BC′D的法向量为$\overrightarrow{n_2}=({x_2},{y_2},{z_2})$,则$\left\{\begin{array}{l}\overrightarrow{n_2}⊥\overrightarrow{BC′}\\ \overrightarrow{n_2}⊥\overrightarrow{C′D}\end{array}\right.$,
即$\left\{\begin{array}{l}\overrightarrow{n_2}•\overrightarrow{BC′}=0\\ \overrightarrow{n_2}•\overrightarrow{C′D}=0\end{array}\right.$,$\left\{\begin{array}{l}-{y_2}+{z_2}=0\\ \frac{{\sqrt{3}}}{2}{x_2}+\frac{1}{2}{y_2}-{z_2}=0\end{array}\right.$,
令z2=1,则y2=1,${x_2}=\frac{{\sqrt{3}}}{3}$,∴$\overrightarrow{n_2}=(\frac{{\sqrt{3}}}{3},1,1)$…(10分)
∴$cos\left?{\overrightarrow{n_1},\overrightarrow{n_2}}\right>=\frac{{\sqrt{3}×\frac{{\sqrt{3}}}{3}+(-1)×1+1×1}}{{\sqrt{3+1+1}•\sqrt{\frac{1}{3}+1+1}}}=\frac{1}{{\sqrt{5}•\sqrt{\frac{7}{3}}}}=\frac{{\sqrt{105}}}{35}$,
二面角A-C′D-B的余弦值为${-}\frac{{\sqrt{105}}}{35}$.…(12分)
点评 本题考查二面角的平面角的求法,平面与平面垂直的判定定理,考查空间想象能力以及计算能力.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
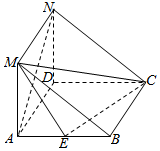 如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ABCD是菱形,∠DAB=60°,AD=2,侧面ADNM是矩形,AM=1.E是AB的中点.
如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ABCD是菱形,∠DAB=60°,AD=2,侧面ADNM是矩形,AM=1.E是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{7}{9}$ | B. | -$\frac{1}{9}$ | C. | $\frac{1}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9,18,3 | B. | 10,15,5 | C. | 10,17,3 | D. | 9,16,5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,四边形ABCD是腰长为2的等腰梯形,其上底长为2,下底长为4,E是腰BC上一点,P为上底CD上一点,且$\overrightarrow{BE}$=$λ\overrightarrow{BC}$,$\overrightarrow{DP}$=$λ\overrightarrow{DC}$,λ∈[0,1],则$\overrightarrow{AP}$•$\overrightarrow{AE}$的取值范围是[4,10].
如图所示,四边形ABCD是腰长为2的等腰梯形,其上底长为2,下底长为4,E是腰BC上一点,P为上底CD上一点,且$\overrightarrow{BE}$=$λ\overrightarrow{BC}$,$\overrightarrow{DP}$=$λ\overrightarrow{DC}$,λ∈[0,1],则$\overrightarrow{AP}$•$\overrightarrow{AE}$的取值范围是[4,10].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com