${∫} {-2}^{-1}$$\frac{2}{x}$dx=( )A．-ln2B．ln2C．-2ln2D．2ln2 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

13．${∫}_{-2}^{-1}$$\frac{2}{x}$dx=（　　）

A．

-ln2

B．

ln2

C．

-2ln2

D．

2ln2

分析由${∫}_{-2}^{-1}$$\frac{2}{x}$dx=-${∫}_{1}^{2}$$\frac{2}{x}$dx，再根据定积分的计算法则计算即可．

解答解：${∫}_{-2}^{-1}$$\frac{2}{x}$dx=-${∫}_{1}^{2}$$\frac{2}{x}$dx=-2lnx|${\;}_{1}^{2}$=-2ln2，
故选：C．

点评本题考查了定积分的计算，关键是求出原函数，属于基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

3．某洗衣机生产流水线上有三条不同的作业线，每条作业线上的质量指标分别为x，y，z，用综合指标S=x+y+z评价该洗衣机的等级．若S≥5，则该洗衣机为特等品；若4≤S≤5，则该洗衣机为一等品；若S＜4，则该洗衣机不合格．现从这一批洗衣机中，随机抽取10台作为样本，其质量指标列表如下：

产品编号	A₁	A₂	A₃	A₄	A₅
质量指标（x，y，z）	（1，1，2）	（2，1，1）	（2，2，2）	（1，1，1）	（1，2，1）
产品编号	A₆	A₇	A₈	A₉	A₁₀
质量指标（x，y，z）	（1，2，2）	（2，1，1）	（2，2，1）	（1，1，1）	（2，1，2）

（1）利用上表提供的样本数据估计该批产品的一等品率；
（2）从编号为A₁到A₆的6台洗衣机中，随机抽取2台，
①用产品编号列出所有可能的结果；
②设事件B为“在取出的2台洗衣机中，恰有一台是一等品一台不合格”，求事件B发生的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

4．f（x）=$\left\{\begin{array}{l}{\frac{\sqrt{x+1}-1}{x}，x≠0}\\{0，x=0}\end{array}\right.$，则x=0是（　　）

A．

可去间断点

B．

无穷间断点

C．

连续点

D．

跳跃间断点

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

1．设函数f（x）=$\left\{\begin{array}{l}{{e}^{x-1}，x＜1}\\{lo{g}_{2}x，x≥1}\end{array}\right.$，则使得f（x）≤1成立的x的取值范围是（-∞，2]．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

8．

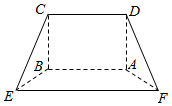如图，在多面体ABCDEF中，四边形ABCD是矩形，四边形ABEF为等腰梯形，且AB∥EF，AF=2，EF=2AB=4AD=4$\sqrt{2}$，平面ABCD⊥平面ABEF．
（1）求证：BE⊥DF；
（2）求二面角E-DF-A的大小．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

18．如图是一个程序框图，则输出的S的值是63．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

5．在平面四边形ACBD（图①）中，△ABC与△ABD均为直角三角形且有公共斜边AB，设AB=2，∠BAD=30°，∠BAC=45°，将△ABC沿AB折起，构成如图②所示的三棱锥C′-ABC，且使$C'D=\sqrt{2}$．
（Ⅰ）求证：平面C′AB⊥平面DAB；
（Ⅱ）求二面角A-C′D-B的余弦值．