
| 产品编号 | A1 | A2 | A3 | A4 | A5 |
| 质量指标(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
| 产品编号 | A6 | A7 | A8 | A9 | A10 |
| 质量指标(x,y,z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
分析 (1)计算10台洗衣机的综合指标S,由此能估计该批洗衣机的特等品率.
(2)①从A1到${{A}_{6}}_{\;}^{\;}$这6台洗衣机中,随机抽取2台,利用列举法能求出所有可能的结果.
②设事件B为“在取出的2台洗衣机中,恰有一台是一等品一台不合格”,利用列举法求出事件B发生的所有可能结果,由此能求出P(B).
解答 解:(1)计算10台洗衣机的综合指标S,如下表:
| 产品编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| S | 4 | 4 | 6 | 3 | 4 | 5 | 4 | 5 | 3 | 5 |
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
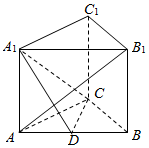 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,AB1⊥平面A1CD,AC⊥BC,D为AB中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,AB1⊥平面A1CD,AC⊥BC,D为AB中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ①② | C. | ②③ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最大值无最小值 | B. | 有最小值无最大值 | ||
| C. | 既有最大值又有最小值 | D. | 既无最大值也无最小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
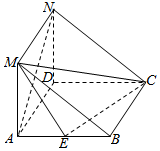 如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ABCD是菱形,∠DAB=60°,AD=2,侧面ADNM是矩形,AM=1.E是AB的中点.
如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ABCD是菱形,∠DAB=60°,AD=2,侧面ADNM是矩形,AM=1.E是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com