
分析 由题意画出图形,由题意可得,满足条件的P点在平面ABB1A1内,利用椭圆定义求出P的轨迹,得到到AB距离最大的P点到AB的距离为12,即四棱锥P-ABCD的高为12,然后代入棱锥体积公式得答案.
解答 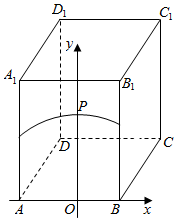 解:如图由题意可知,当P点位于平面ABB1A1上时,能使四棱锥P-ABCD的体积最大,
解:如图由题意可知,当P点位于平面ABB1A1上时,能使四棱锥P-ABCD的体积最大,
在平面ABB1A1内,以AB所在直线为x轴,以AB的垂直平分线为y轴建系,
∵AB=10,且|PA|+|PB|=26>10,
∴P在以A,B为焦点的椭圆上,
且a=13,c=5,∴b2=a2-c2=132-52=122,
则平面ABB1A1内,满足|PA|+|PB|=26,且到AB距离最大的P点到AB的距离为12,
∴四棱锥P-ABCD的体积的最大值为$\frac{1}{3}×10×10×12=400$.
故答案为:400.
点评 本题考查棱锥的体积,考查了数形结合的解题思想方法,利用椭圆定义求出满足条件的P点是解答该题的关键,是中档题.


科目:高中数学 来源: 题型:解答题
| 高校 | 相关人数 | 抽取人数 |
| A | 54 | x |
| B | 36 | 2 |
| C | 72 | y |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-∞,-1]∪(0,1) | C. | [-1,4] | D. | (-∞,-1]∪[0,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 可去间断点 | B. | 无穷间断点 | C. | 连续点 | D. | 跳跃间断点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
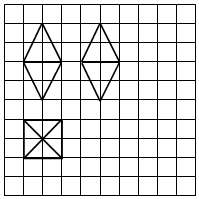 如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )| A. | 16 | B. | 8$\sqrt{5}$ | C. | 32 | D. | 16$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
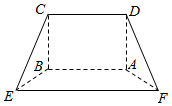 如图,在多面体ABCDEF中,四边形ABCD是矩形,四边形ABEF为等腰梯形,且AB∥EF,AF=2,EF=2AB=4AD=4$\sqrt{2}$,平面ABCD⊥平面ABEF.
如图,在多面体ABCDEF中,四边形ABCD是矩形,四边形ABEF为等腰梯形,且AB∥EF,AF=2,EF=2AB=4AD=4$\sqrt{2}$,平面ABCD⊥平面ABEF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
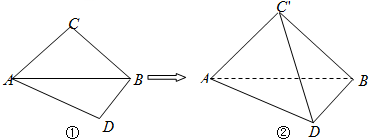
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com