
分析 (Ⅰ)如果学生只吃食物Axkg,从而得不等式组$\left\{\begin{array}{l}{60≤60x≤90}\\{18≤9x≤27}\end{array}\right.$,是否有解即可;
(Ⅱ)由题意,设学生每天吃食物Axkg,食物Bykg;从而得到目标函数z=20x+15y;线性约束条件$\left\{\begin{array}{l}{60≤60x+30y≤90}\\{18≤9x+27y≤27}\\{x≥0}\\{y≥0}\end{array}\right.$,从而利用线性规划求解即可.
解答 解:(Ⅰ)如果学生只吃食物Axkg,
则$\left\{\begin{array}{l}{60≤60x≤90}\\{18≤9x≤27}\end{array}\right.$,
无解,
故不符合营养学家的建议;
(Ⅱ)由题意,设学生每天吃食物Axkg,食物Bykg;
则z=20x+15y;
$\left\{\begin{array}{l}{60≤60x+30y≤90}\\{18≤9x+27y≤27}\\{x≥0}\\{y≥0}\end{array}\right.$
作平面区域如下,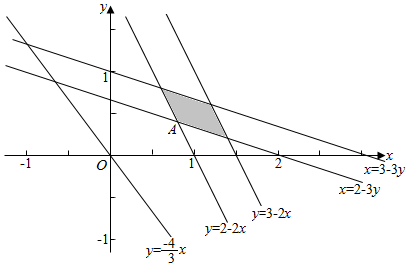 ,
,
由$\left\{\begin{array}{l}{x=2-3y}\\{y=2-2x}\end{array}\right.$解得,x=$\frac{4}{5}$,y=$\frac{2}{5}$;
故z=20×$\frac{4}{5}$+15×$\frac{2}{5}$=22;
答:学生每天吃0.8千克食物A,0.4千克食物B,既能符合营养学家的建议又花费最少.
最低需要花费22元.
点评 本题考查了线性规划在实际问题中的应用,属于中档题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
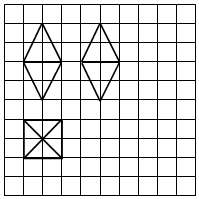 如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )| A. | 16 | B. | 8$\sqrt{5}$ | C. | 32 | D. | 16$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
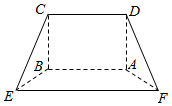 如图,在多面体ABCDEF中,四边形ABCD是矩形,四边形ABEF为等腰梯形,且AB∥EF,AF=2,EF=2AB=4AD=4$\sqrt{2}$,平面ABCD⊥平面ABEF.
如图,在多面体ABCDEF中,四边形ABCD是矩形,四边形ABEF为等腰梯形,且AB∥EF,AF=2,EF=2AB=4AD=4$\sqrt{2}$,平面ABCD⊥平面ABEF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
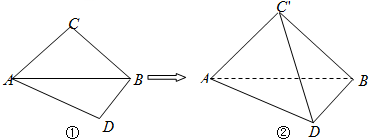
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}{e}^{2}$ | B. | 3e2 | C. | 6e2 | D. | 9e2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 广告费用x(万元) | 2 | 3 | 5 | 6 |
| 销售利润y(万元) | 5 | 7 | 9 | 11 |
| A. | $\hat b>0$ | B. | $\hat a>0$ | C. | 直线l过点(4,8) | D. | 直线l过点(2,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com