考点:平面与平面平行的判定,直线与平面垂直的判定,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)连接B1D1,根据平行线的传递性即可得到BD∥EF;
(2)容易说明BD⊥AC,BD⊥AA1,从而得到BD⊥平面AA1C1C;
(3)由已知条件能够得到MN∥EF,从而MN∥平面BDFE,设AC交BD于O,A1C1交MN于Q,交EF于P,能够说明AQ∥OP,从而得到AQ∥平面BDFE,这样即可得到平面AMN∥平面BDFE.
解答:
证:(1)如图,连接B
1D
1,由已知条件知:EF∥B
1D
1,
又BD∥B
1D
1,∴BD∥EF;
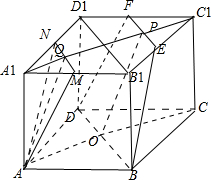
(2)由已知条件知:AA
1⊥平面ABCD,BD?平面ABCD,
∴AA
1⊥BD,即BD⊥AA
1;
又BD⊥AC,AA
1∩AC=A,
∴BD⊥平面AA
1C
1C;
(3)设AC交BD于O,A
1C
1交MN于Q,交EF于P,则PQ∥AO,且PQ=AO,
∴四边形AOPQ是平行四边形,
∴AQ∥OP,OP?平面BDFE;
∴AQ∥平面BDFE,
又MN∥EF,EF?平面BDFE,
∴MN∥平面BDFE,MN∩AQ=Q;
∴平面AMN∥平面BDFE.
点评:考查平行线的传递性,线面垂直的性质及判定定理,线面平行的判定定理,面面平行的判定定理.

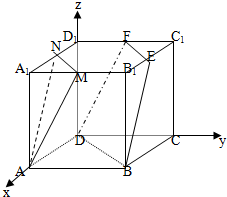 如图,在正方体ABCD-A1B1C1D1中,M、N分别是棱A1B1、A1D1的中点,E、F分别是棱B1C1、C1D1的中点.求证:
如图,在正方体ABCD-A1B1C1D1中,M、N分别是棱A1B1、A1D1的中点,E、F分别是棱B1C1、C1D1的中点.求证: (2)由已知条件知:AA1⊥平面ABCD,BD?平面ABCD,
(2)由已知条件知:AA1⊥平面ABCD,BD?平面ABCD,
