
(12分)在平面α内有△ABC,在平面α外有点S,斜线SA⊥AC,SB⊥BC,且
斜线SA、SB与平面α所成角相等。
(1)求证:AC=BC
(2)又设点S到α的距离为4cm,AC⊥BC且AB=6cm,求S与AB的距离。
科目:高中数学 来源: 题型:解答题
(本小题共12分)如图,四棱锥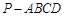 的底面是直角梯形,
的底面是直角梯形,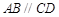 ,
, ,
, 和
和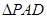 是两个边长为
是两个边长为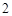 的正三角形,
的正三角形,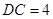 ,
,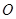 为
为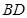 的中点,
的中点,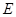 为
为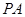 的中点.
的中点.
(Ⅰ)求证: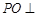 平面
平面 ;
;
(Ⅱ)求证: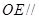 平面
平面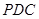 ;
;
(Ⅲ)求直线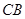 与平面
与平面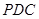 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分15分)在直角梯形A1A2A3D中,A1A2⊥A1D,A1A2⊥A2A3,且B,C分别是边A1A2,A2A3上的一点,沿线段 BC,CD,DB分别将△BCA2,△CDA3,△DBA1翻折上去恰好使A1,A2,A3重合于一点A。
BC,CD,DB分别将△BCA2,△CDA3,△DBA1翻折上去恰好使A1,A2,A3重合于一点A。
(Ⅰ)求证:AB⊥CD;
(Ⅱ)已知A1D=10,A1A2=8,求二面角A-BC-D的余弦值。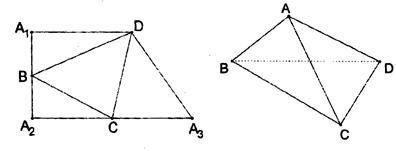
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)(理)如图9-6-6,矩形ABCD中,A B=1,BC=a,PA⊥平面ABCD
B=1,BC=a,PA⊥平面ABCD
(1)问BC边上是否存在Q点,使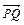 ⊥
⊥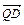 ,说明理由.
,说明理由.
(2)问当Q点惟一,且cos<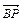 ,
,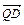 >=
>=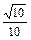 时,求点P的位置.
时,求点P的位置.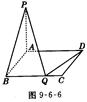
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图,已知四棱锥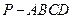 中,侧棱
中,侧棱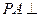 平面
平面 ,底面
,底面 是平行四边形,
是平行四边形, ,
,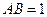 ,
, ,
, 分别是
分别是 的中点.
的中点.
(1)求证: 平面
平面
(2)当平面 与底面
与底面 所成二面角为
所成二面角为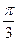 时,求二面角
时,求二面角 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
平面α经过三点A(-1,0,1),B(1,1,2),C(2,-1,0),则下列向量中与平面α的法向量不垂直的是( )
A.(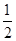 ,-1,-1) ,-1,-1) | B.(6,-2,-2) |
| C.(4,2,2) | D.(-1,1,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com