
(12分)(理)如图9-6-6,矩形ABCD中,A B=1,BC=a,PA⊥平面ABCD
B=1,BC=a,PA⊥平面ABCD
(1)问BC边上是否存在Q点,使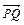 ⊥
⊥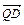 ,说明理由.
,说明理由.
(2)问当Q点惟一,且cos<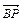 ,
,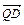 >=
>=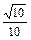 时,求点P的位置.
时,求点P的位置.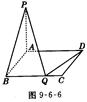
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:高中数学 来源: 题型:解答题
如图,在平行四边形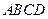 中,
中,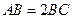 ,
,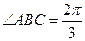 ,
,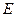 为线段
为线段 的中线,将△
的中线,将△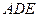 沿
沿 直线
直线 翻折成△
翻折成△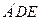 ,使平面
,使平面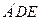 ⊥平面
⊥平面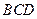 ,
,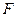 为线
为线 段
段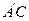 的中点.
的中点.
(1)求证: ∥平面
∥平面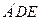 ;
;
(2)设 为线段
为线段 的中点,求直线
的中点,求直线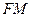 与平面
与平面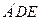 所成角的余弦值.
所成角的余弦值.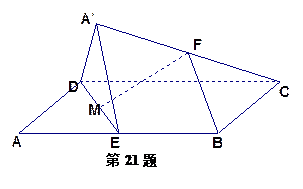
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
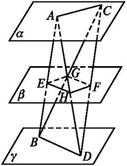
如图所示,两条异面直线AB,CD与三个平行平面α,β,γ分别相交于A,E,B及
C,F,D,又AD、BC与平面β的交点为H,G.
求证:四边形EHFG为平行四边形。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)在平面α内有△ABC,在平面α外有点S,斜线SA⊥AC,SB⊥BC,且
斜线SA、SB与平面α所成角相等。
(1)求证:AC=BC
(2)又设点S到α的距离为4cm,AC⊥BC且AB=6cm,求S与AB的距离。
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图所示,ABCD-A1B1C1D1是棱长为6的正方体,E,F分别是棱AB,BC上的动点,且AE=BF.当A1,E,F,C1共面时,平面A1DE与平面C1DF所成二面角的余弦值为( )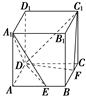
A.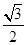 | B.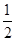 | C.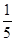 | D.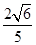 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
在三棱柱ABC-A1B1C1中,底面为边长为1的正三角形,侧棱AA1⊥底面ABC,点D在棱BB1上,且BD=1,若AD与平面AA1C1C所成的角为α,则sinα的值为( )
A.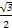 | B.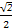 | C. | D.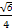 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com