
| 微信群数量 | 频数 | 频率 |
| 0至5个 | 0 | 0 |
| 6至10个 | 30 | 0.3 |
| 11至15个 | 30 | 0.3 |
| 16至20个 | a | c |
| 20个以上 | 5 | b |
| 合计 | 100 | 1 |
分析 (Ⅰ)由频率分布表能求出a,b,c的值.
(Ⅱ)依题意可知,微信群个数超过15个的概率为p=$\frac{2}{5}$. X的所有可能取值0,1,2,3.分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(Ⅰ)由已知得:0+30+30+a+5=100,解得a=35,
∴$b=\frac{5}{100}=0.05,c=\frac{35}{100}=0.35$.…(3分)
(Ⅱ)依题意可知,微信群个数超过15个的概率为p=$\frac{2}{5}$. …(4分)
X的所有可能取值0,1,2,3. …(5分)
则P(X=0)=${C}_{3}^{0}(\frac{2}{5})^{0}(1-\frac{2}{5})^{3}$═$\frac{27}{125}$,
P(X=1)=${C}_{3}^{1}(\frac{2}{5})(1-\frac{2}{5})^{2}$=$\frac{54}{125}$,
P(X=2)=${C}_{3}^{2}(\frac{2}{5})^{2}(1-\frac{2}{5})$=$\frac{36}{125}$,
P(X=3)=${C}_{3}^{3}(\frac{2}{5})^{3}(1-\frac{2}{5})^{0}$=$\frac{8}{125}$. …(8分)
其分布列如下:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{27}{125}$ | $\frac{54}{125}$ | $\frac{36}{125}$ | $\frac{8}{125}$ |
点评 本题考查概率的求法,考查频率分布表、离散型随机变量的分布列、数学期望等基础知识,考查运算求解能力、数据处理能力,考查化归与转化思想、函数与方程思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,已知DC∥AB,DC=2AB,E为棱PD的中点.
在四棱锥P-ABCD中,已知DC∥AB,DC=2AB,E为棱PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
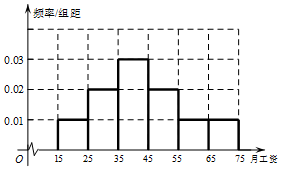 为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:| 月工资 (单位:百元) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 男员工数 | 1 | 8 | 10 | 6 | 4 | 4 |
| 女员工数 | 4 | 2 | 5 | 4 | 1 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
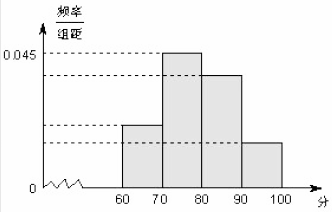
| 分数段 | 频数 | |
| [60,70) | p | |
| [70,80) | 90 | |
| [80,90) | 60 | |
| [90,100] | 20 | q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com