
分析 (Ⅰ)求出切点坐标,求出函数的导数,计算斜率,代入直线方程即可;
(Ⅱ)问题转化为证e2•x(1+lnx)>$\frac{xe}{{e}^{x}}$-2,设g(x)=e2•x(1+lnx),(x>0),h(x)=$\frac{xe}{{e}^{x}}$-2,(x>0),根据函数的单调性分别求出g(x)的最小值和h(x)的最大值即可.
解答 解:(Ⅰ)因为f(1)=e(1+0)=e,所以切点坐标为(1,e)------------------------------(1分)
又f′(x)=ex(1+lnx+$\frac{1}{x}$),----------------------------------------(3分)
所以f′(1)=e(1+1+0)=2e,即切线斜率为2e,------------------------------------(4分)
因此切线方程为y-e=2e(x-1),即2ex-y-e=0--------------------------------(5分)
(Ⅱ)要证e2f(x)>e-$\frac{{2e}^{x}}{x}$,即证e2•ex(1+lnx)>e-$\frac{{2e}^{x}}{x}$,
由于x>0,ex>0,所以即证e2•x(1+lnx)>$\frac{xe}{{e}^{x}}$-2----------------------------(7分)
设g(x)=e2•x(1+lnx),(x>0),h(x)=$\frac{xe}{{e}^{x}}$-2,(x>0),
则g′(x)=e2(2+lnx),
当0<x<e-2时,g′(x)<0,g(x)单调递减,
当x>e-2时,g′(x)>0,g(x)单调递增;
故g(x)min=g(e-2)=-1,即g(x)≥-1,当x=e-2时等号成立;---------------------------------------------------(9分)
又h′(x)=$\frac{e(1-x)}{{e}^{x}}$,当0<x<1时,h′(x)>0,h(x)单调递增;
当x>1时,h′(x)<0,h(x)在(0,1)单调递减
故h(x)max=h(1)=-1,
即h(x)≤-1,当x=1时等号成立;-------------------------------------------------(11分)
所以g(x)>h(x)在(0,+∞)上恒成立,
即e2•x(1+lnx)>$\frac{xe}{{e}^{x}}$-2,
故e2f(x)>e-$\frac{2{e}^{x}}{x}$.------------------------------------------------------(12分)
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| P(K2>k0) | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
| 捐款超过500元 | a=30 | b | |
| 捐款不超过500元 | c | d=6 | |
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
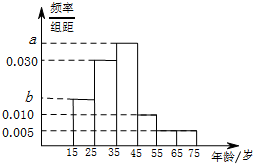 2016年全国两会,即中华人民共和国第十二届全国人民代表大会第四次会议和中国人民政治协商会议第十二届全国委员会第四次会议,分别于2016年3月5日和3月3日在北京开幕.为了解哪些人更关注两会,某机构随抽取了年龄在15~75岁之间的100人进行调查,并按年龄绘制的频率分布直方图如图所示,其分组区间为:[15,25),[25,35),[35,45),[55,65),[65,75].把年龄落在区间[15,35)和[35,75]内的人分别称为“青少年人”和“中老年人”,经统计“青少年人”和“中老年人”的人数之比为9:11.
2016年全国两会,即中华人民共和国第十二届全国人民代表大会第四次会议和中国人民政治协商会议第十二届全国委员会第四次会议,分别于2016年3月5日和3月3日在北京开幕.为了解哪些人更关注两会,某机构随抽取了年龄在15~75岁之间的100人进行调查,并按年龄绘制的频率分布直方图如图所示,其分组区间为:[15,25),[25,35),[35,45),[55,65),[65,75].把年龄落在区间[15,35)和[35,75]内的人分别称为“青少年人”和“中老年人”,经统计“青少年人”和“中老年人”的人数之比为9:11.| 关注 | 不关注 | 合计 | |
| 青少年人 | 15 | ||
| 中老年人 | |||
| 合计 | 50 | 50 | 100 |
| P(K2≥k0) | 0.05 | 0.01 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com