
分析 (1)把已知的数列递推式两边平方,即可证得{$\frac{1}{a_{n}^{2}}$}为等差数列;
(2)由(1)中的等差数列求出通项公式,进一步可得数列{an}的通项公式.
解答 (1)证明:由$\frac{1}{a_{n+1}}$=$\sqrt{3+\frac{1}{a_{n}^{2}}}$,得$\frac{1}{{{a}_{n+1}}^{2}}=3+\frac{1}{{{a}_{n}}^{2}}$,
即$\frac{1}{{{a}_{n+1}}^{2}}-\frac{1}{{{a}_{n}}^{2}}=3$,
又a1=1,∴$\frac{1}{{{a}_{1}}^{2}}=1$,
则数列{$\frac{1}{a_{n}^{2}}$}为以1为首项,以3为公差的等差数列;
(2)解:∵数列{$\frac{1}{a_{n}^{2}}$}为以1为首项,以3为公差的等差数列,
∴$\frac{1}{{{a}_{n}}^{2}}=1+3(n-1)=3n-2$,
则${{a}_{n}}^{2}=\frac{1}{3n-2}$,又an>0,
∴${a}_{n}=\sqrt{\frac{1}{3n-2}}$.
点评 本题考查了数列递推式,考查了等差关系的确定,训练了等差数列通项公式的求法,是中档题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 编号 | 甲 | 乙 | 丙 | 丁 | 戊 |
| 身高x(cm) | 166 | 170 | 172 | 174 | 178 |
| 体重y(kg) | 55 | 60 | 65 | 65 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
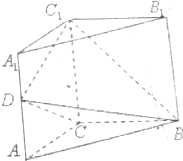 如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=$\frac{1}{2}$AA1,D是棱AA1上的动点.
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=$\frac{1}{2}$AA1,D是棱AA1上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com