
【题目】如图,EB垂直于菱形ABCD所在平面,且EB=BC=2,∠BAD=60°,点G、H分别为线段CD、DA的中点,M为BE上的动点.
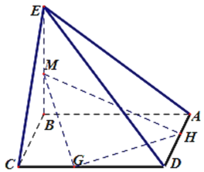
(Ⅰ)求证:GH⊥DM;
(Ⅱ)当三棱锥D﹣MGH的体积最大时,求三角形MGH的面积.
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】
(Ⅰ)由BE⊥AC,BD⊥AC得到AC⊥平面BDE,再由GH∥AC,得到GH⊥平面BDE,故得证.
(Ⅱ)由于BM⊥平面ABCD,故![]() ,当点M与点E重合时,BM取得最大值,故(VD﹣MGH)max,即得解.
,当点M与点E重合时,BM取得最大值,故(VD﹣MGH)max,即得解.
(Ⅰ)证明:连接AC、BD相交于点O.
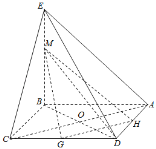
∵BE⊥平面ABCD.而AC平面ABCD,∴BE⊥AC.
又∵四边形ABCD为菱形,∴BD⊥AC.
∵BD∩BE=B,∴AC⊥平面BDE.
∵G、H分别为DC、AD的中点,
∴GH∥AC,则GH⊥平面BDE.
而DM平面BDE,∴GH⊥DM.
(II)解:菱形ABCD中,∠BAD=60°,得,∠ADC=120°.
∵DG=DH=1,
∴S△DGH═![]() ,
,
∵BE⊥平面ABCD,即BM⊥平面ABCD,
∴![]() BM.
BM.
当点M与点E重合时,BM取得最大值2,此时(VD﹣MGH)max![]() .
.
且MG=MH![]() ,GH
,GH![]() ,则S△MGH
,则S△MGH![]()


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线C:![]() 的焦点为F,过F的直线
的焦点为F,过F的直线![]() 交抛物线C于A,B两点.
交抛物线C于A,B两点.
(1)求线段AF的中点M的轨迹方程;
(2)已知△AOB的面积是△BOF面积的3倍,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且以椭圆
,且以椭圆![]() 的两焦点和短轴的一个端点为顶点的三角形的周长恰为
的两焦点和短轴的一个端点为顶点的三角形的周长恰为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)动直线![]() 与抛椭圆
与抛椭圆![]() 相交于
相交于![]() ,
,![]() 两点,问:在
两点,问:在![]() 轴上是否存在定点
轴上是否存在定点![]() (其中
(其中![]() ,使得向量
,使得向量![]() 与向量
与向量![]() 共线(其中
共线(其中![]() 为坐标原点)?若存在,求出点
为坐标原点)?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将420名工人编号为:001,002,![]() ,420,采用系统抽样的方法抽取一个容量为60的样本,且随机抽得的号码为005.这420名工人来自三个工厂,从001到200为
,420,采用系统抽样的方法抽取一个容量为60的样本,且随机抽得的号码为005.这420名工人来自三个工厂,从001到200为![]() 工厂,从201到355为
工厂,从201到355为![]() 工厂,从356到420为
工厂,从356到420为![]() 工厂,则三个工厂被抽中的工人数依次为( )
工厂,则三个工厂被抽中的工人数依次为( )
A.28,23,9B.27,23,10C.27,22,11D.28,22,10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市食品药品监督管理局开展2020年春季快递餐饮安全检查,对本市的8个快递配餐点进行了原料采购加工标准和卫生标准的检查和评分,其评分情况如表所示:
快递配餐点编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
原料采购加工标准评分 | 82 | 75 | 70 | 66 | 83 | 93 | 95 | 100 |
卫生标准评分 | 81 | 79 | 77 | 75 | 82 | 83 | 84 | 87 |
(1)已知![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(精确到0.1)
的线性回归方程;(精确到0.1)
(2)现从8个被检查点中任意抽取两个组成一组,若两个点的原料采购加工标准和卫生标准的评分均超过80分,则组成“快递标兵配餐点”,求该组被评为“快递标兵配餐点”的概率.
参考公式: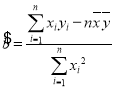 ,
,![]() ;参考数据:
;参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,直线l:![]() ,P为直线l上一点,且点P在极轴上方
,P为直线l上一点,且点P在极轴上方![]() 以OP为一边作正三角形
以OP为一边作正三角形![]() 逆时针方向
逆时针方向![]() ,且
,且![]() 面积为
面积为![]() .
.
![]() 求Q点的极坐标;
求Q点的极坐标;
![]() 求
求![]() 外接圆的极坐标方程,并判断直线l与
外接圆的极坐标方程,并判断直线l与![]() 外接圆的位置关系.
外接圆的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com