
| A. | 3 | B. | 6 | C. | 2 | D. | m |
分析 逐步分析框图中的各框语句的功能,第二步条件结构是比较a,b的大小,并将a,b中的较小值保存在变量m中,第三步条件结构是比较a,c的大小,并将a,c中的较小值保存在变量m中,故变量m的值最终为a,b,c中的最小值,否则输出“无解”.由此不难推断执行这个算法的结果.
解答 解:逐步分析算法中的各语句的功能,
第一个条件结构是比较a,b的大小,
并将a,b中的较小值保存在变量m中,
第二个条件结构是比较a,c的大小,
并将a,c中的较小值保存在变量m中,
故变量m的值最终为a,b,c中的最小值.
由此程序的功能为求a,b,c三个数的最小数,∴m=2.
故选C.
点评 要判断程序的功能就要对程序的流程图(伪代码)逐步进行分析,分析出各变量值的变化情况,特别是输出变量值的变化情况,就不难得到正确的答案.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:选择题
| A. | -57 | B. | -37 | C. | 16 | D. | 57 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
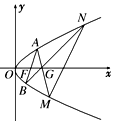 如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)任作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).
如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)任作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | $\frac{5π}{4}$ | C. | $\frac{{\sqrt{3}π}}{3}$ | D. | $\frac{{2\sqrt{3}}}{9}{π^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{27},+∞})$ | B. | $({\frac{4}{27},+∞})$ | C. | $[{\frac{1}{27},+∞})$ | D. | $[{\frac{4}{27},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21 | B. | 1 | C. | 3 | D. | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,4) | B. | (1,-4) | C. | (-1,-4) | D. | (1,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com