
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
分析 先求出基本事件总数n=${C}_{3}^{2}{C}_{1}^{1}{A}_{2}^{2}$=6,再求出甲、乙两名交警在同一路口包含的基本事件m=${A}_{2}^{2}$=2,由此利用对立事件概率计算公式能求出甲、乙两名交警不在同一路口的概率.
解答 解:将甲、乙、丙三名交警安排到某商业中心附近的两个不同路口突击检查,每个路口至少一人,
基本事件总数n=${C}_{3}^{2}{C}_{1}^{1}{A}_{2}^{2}$=6,
甲、乙两名交警在同一路口包含的基本事件m=${A}_{2}^{2}$=2
∴甲、乙两名交警不在同一路口的概率p=$1-\frac{2}{6}$=$\frac{2}{3}$.
故选:D.
点评 本题考查古典概型、概率的求法等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、集合思想,是基础题.


科目:高中数学 来源: 题型:解答题
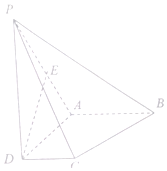 如图,四棱锥P-ABCD中,底面ABCD是梯形,∠ADC=∠BAD=90°且AB=AD=PD=2CD=2,PD⊥平面ABCD,E是PA中点.
如图,四棱锥P-ABCD中,底面ABCD是梯形,∠ADC=∠BAD=90°且AB=AD=PD=2CD=2,PD⊥平面ABCD,E是PA中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 2 | D. | m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
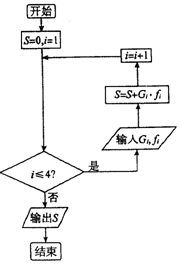 为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,得到如下的频率分布表:
为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,得到如下的频率分布表:| 序号 (i) | 分组 (分数) | 组中值 (Gi) | 频数 (人数) | 频率 (Fi) |
| 1 | [60,70) | 65 | ① | 0.10 |
| 2 | [70,80) | 75 | 20 | ② |
| 3 | [80,90) | 85 | ③ | 0.20 |
| 4 | [90,100) | 95 | ④ | ⑤ |
| 合计 | 50 | 1 | ||
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $-\frac{3}{2}$ | C. | -2 | D. | -6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com