
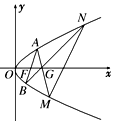
 如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)任作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).
如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)任作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).分析 (1)代入抛物线方程,利用韦达定理即可求得y1y2常数,-2p2=-8,即可求得p的值;
(2)求出y3•y4=-2p2,y1•y3=-p2,即可求出直线AB与直线MN斜率之比.
解答 解:(1)证明:设直线AM的方程为x=my+p,
代入抛物线方程$\left\{\begin{array}{l}{x=my+p}\\{{y}^{2}=2px}\end{array}\right.$,整理得y2-2mpy-2p2=0,
由韦达定理可知:y1•y2=-2p2为定值;
由y1•y2=-2p2=-8,
∴p=2,
∴抛物线C:y2=4x;
(Ⅱ)证明设B(x3,y3),N(x4,y4),
设直线NB:x=ny+p,代入抛物线方程,可得,y2-2pny-2p2=0,
则y3•y4=-2p2,同理可知y1•y2=-2p2,
y1•y3=-p2,
∴直线AB与直线MN斜率之比为$\frac{\frac{2p}{{y}_{1}+{y}_{3}}}{\frac{2p}{{y}_{2}+{y}_{4}}}$=$\frac{{y}_{2}+{y}_{4}}{{y}_{1}+{y}_{2}}$=$\frac{\frac{-2p}{{y}_{1}{y}_{3}}({y}_{1}+{y}_{3})}{{y}_{1}+{y}_{3}}$=2.
点评 本题考查抛物线的方程与性质,直线与抛物线的位置关系,韦达定理的应用,考查学生的计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
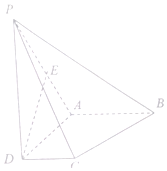 如图,四棱锥P-ABCD中,底面ABCD是梯形,∠ADC=∠BAD=90°且AB=AD=PD=2CD=2,PD⊥平面ABCD,E是PA中点.
如图,四棱锥P-ABCD中,底面ABCD是梯形,∠ADC=∠BAD=90°且AB=AD=PD=2CD=2,PD⊥平面ABCD,E是PA中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 满意 | 不满意 | 合计 | |
| 男 | 10 | 20 | 30 |
| 女 | 15 | 5 | 20 |
| 合计 | 25 | 25 | 50 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
| A. | 有95%的把握认为对电视节目的满意度与性别无关 | |
| B. | 有99%的把握认为对电视节目的满意度与性别无关 | |
| C. | 有99%的把握认为对电视节目的满意度与性别有关 | |
| D. | 有95%的把握认为对电视节目的满意度与性别有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-$\sqrt{3}$]∪[$\sqrt{3}$,2) | B. | [-2,-$\sqrt{3}$)∪($\sqrt{3}$,2] | C. | [-2,2] | D. | (-$\sqrt{3}$,$\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | △ABC的内部 | B. | △ABC的外部 | C. | P在线段AC上 | D. | P在线段AB上 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 2 | D. | m |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $-\frac{3}{2}$ | C. | -2 | D. | -6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com