
工厂有一段旧墙长 m,现准备利用这段旧墙为一面,建造平面图形为矩形,面积为
m,现准备利用这段旧墙为一面,建造平面图形为矩形,面积为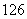 m2的厂房,工程条件是:(1)建1m新墙费用为a元;(2)修1 m旧墙费用是
m2的厂房,工程条件是:(1)建1m新墙费用为a元;(2)修1 m旧墙费用是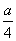 元;(3)拆去1 m旧墙,用所得材料建1m新墙费用为
元;(3)拆去1 m旧墙,用所得材料建1m新墙费用为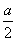 元,经过讨论有两种方案:
元,经过讨论有两种方案:
①利用旧墙的一段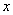
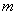 (x<14)为矩形厂房一面的边长;
(x<14)为矩形厂房一面的边长;
②矩形厂房利用旧墙的一面,矩形边长x≥14。
问:如何利用旧墙,即x为多少m时,建墙费用最省?①②两种方案哪种更好?
解:(1)利用旧墙的一段xm(x<14),则修墙费用为x·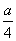 元,将剩余旧墙拆得材料建新墙费用为(14-x)·
元,将剩余旧墙拆得材料建新墙费用为(14-x)·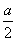 元,其余建新墙的费用为
元,其余建新墙的费用为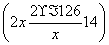 ·a元.
·a元.
总费用y=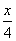 a+
a+ a+
a+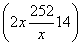 a=a
a=a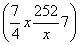 =7a
=7a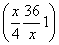 (0<x<14).
(0<x<14).
∴y≥7a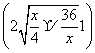 =35a。当且仅当
=35a。当且仅当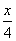 =
=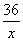 ,即x=12m时,ymin=35a.
,即x=12m时,ymin=35a.
(2)利用旧墙的一面,矩形边长x≥14,则修旧墙费用为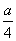 ×14=
×14=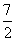 a元,建新墙费用为
a元,建新墙费用为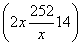 a元.
a元.
总费用y=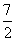 a+
a+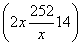 a=
a=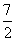 a+2a
a+2a (x≥14).
(x≥14).
由t=x+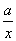 在[
在[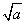 ,+∞)上为增函数,得y1=x+
,+∞)上为增函数,得y1=x+ 在[14,+∞)上为增函数.
在[14,+∞)上为增函数.
∴当x=14m时,ymin=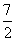 a+2a
a+2a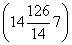 =35.5a.
=35.5a.
综上所述,采用第一种方案,利用旧墙的12m为矩形的一面边长时,建墙费用最省


科目:高中数学 来源: 题型:
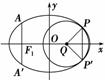
如图,椭圆的中心为原点O,长轴在x轴上,离心率e=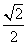 ,
,
过左焦点F1作x轴的垂线交椭圆于A,A′两点,|AA′|=4.
(1)求该椭圆的标准方程;
(2)取垂直于x轴的直线与椭圆相交于不同的两点P,P′,过P,P′作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若PQ⊥P′Q,求圆Q的标准方程.
 |
查看答案和解析>>
科目:高中数学 来源: 题型:
要证a2+b2-1-a2b2≤0,只要证明( )
A.2ab-1-a2b2≤0 B.a2+b2-1-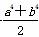 ≤0
≤0
C. 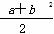 -1-a2b2≤0 D.(a2-1)(b2-1)≥0
-1-a2b2≤0 D.(a2-1)(b2-1)≥0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com