
分析 由已知互相垂直的两条直线,以它建立直角坐标系,求出直线BP与B′P′的方程,找出交点M的M坐标,消掉字母即可得交点M的M轨迹方程.
解答 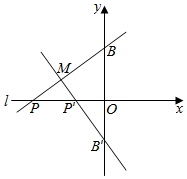 解:以O为原点,BB′为yy轴,l为xxx轴建立如图所示直角坐标系,则B(0,2),B′(0,-2),
解:以O为原点,BB′为yy轴,l为xxx轴建立如图所示直角坐标系,则B(0,2),B′(0,-2),
设P(a,0),a≠0,则由OP•OP′=9,得P′($\frac{9}{a}$,0),
直线BP的方程为$\frac{x}{a}+\frac{y}{2}=1$,即2x+ay-2a=0,
直线B′P′的方程为$\frac{x}{\frac{9}{a}}+\frac{y}{-2}=1$,即2ax-9y-18=0.
设M(x,y),联立$\left\{\begin{array}{l}{2x+ay-2a=0}\\{2ax-9y-18=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{18a}{{a}^{2}+9}}\\{y=\frac{2{a}^{2}-18}{{a}^{2}+9}}\end{array}\right.$,
消去a,可得4x2+9y2=36(x≠0).
∴点M的轨迹是长轴长为6,短轴长为4的椭圆(除去点B、B′).
点评 本题考查轨迹方程的求法,考查取的参数方程,联立方程组求解是关键,属中档题.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:填空题
如图,在长方体ABCD—A1B1C1D1中,AB=3cm,AD=2cm,AA1=1cm,则三棱锥B1—ABD1的体积___________cm3.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:填空题
已知矩形 的顶点都在半径为
的顶点都在半径为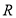 的球
的球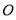 的球面上,且
的球面上,且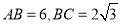 ,棱锥
,棱锥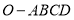 的体积为
的体积为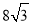 ,则
,则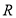 = ________.
= ________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com