
分析 (1)利用圆心和半径,能求出圆的标准方程.
(2)设所求的圆的方程为x2+y2+Dx+Ey+F=0,利用待定系数法能求出圆的方程.
(3)设圆心坐标为(a,b),利用两点间距离公式和圆心在直线上,列出方程组,能求出圆心坐标,从而能求出圆的方程.
(4)由点C(-1,-5)到y轴的距离为1,得到圆半径r=1,由此能求出圆的方程.
解答 解:(1)圆心在原点,半径为6的圆的标准方程为:x2+y2=36.
(2)设所求的圆的方程为x2+y2+Dx+Ey+F=0,
∵圆过三点A(1,1),B(-6,3),C(3,0),
∴$\left\{\begin{array}{l}{1+1+D+E+F=0}\\{36+9-6D+3E+F=0}\\{9+3D+F=0}\end{array}\right.$,
解得D=19,E=45,F=-66,
∴所求圆的方程为x2+y2+19x+45y-66=0.
(3)设圆心坐标为(a,b),
则$\left\{\begin{array}{l}{\sqrt{(a+1)^{2}+(b-3)^{2}}=\sqrt{(a-6)^{2}+(b+1)^{2}}}\\{a+2b=0}\end{array}\right.$,
解得a=$\frac{3}{2}$,b=-$\frac{3}{4}$,
∴$r=\sqrt{(\frac{3}{2}+1)^{2}+(-\frac{3}{4}-3)^{2}}$=$\frac{5\sqrt{13}}{4}$,
∴所求圆的方程为$(x-\frac{3}{2})^{2}+(y+\frac{3}{4})^{2}=\frac{325}{16}$.
(4)∵点C(-1,-5)到y轴的距离为1,
∴圆半径r=1,
∴所求圆的方程为(x+1)2+(y+5)2=1.
点评 本题考查圆的方程的求法,是基础题,解题时要认真审题,注意圆的性质、待定系数法、两点间距离公式的合理运用.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
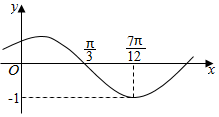 已知函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示,将函数f(x)的图象向左平移$\frac{π}{6}$个单位长度得到函数g(x)的图象,则函数g(x)的解析式为( )
已知函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示,将函数f(x)的图象向左平移$\frac{π}{6}$个单位长度得到函数g(x)的图象,则函数g(x)的解析式为( )| A. | g(x)=sin(2x-$\frac{π}{3}$) | B. | g(x)=sin(2x+$\frac{π}{6}$) | C. | g(x)=-sin(2x-$\frac{π}{3}$) | D. | g(x)=sin(4x+$\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a米 | B. | 2a米 | C. | 3a米 | D. | 4a米 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -60°,(-3,4) | B. | 120°,(-3,4) | C. | 150°,(-3,4) | D. | 120°,(3,-4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{7}$ | C. | $\sqrt{10}$ | D. | $\sqrt{19}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com