
分析 分别根据两角和与差的正弦公式,以及诱导公式,化简计算即可.
解答 解:(1)sin14°cos16°+sin76°•cos74°=sin14°cos16°+cos14°•sin16°=sin30°=$\frac{1}{2}$,
(2)sin(54°-x)cos(36°+x)+cos(54°-x)sin(36°+x)=sin(54°-x+36°+x)=sin90°=1,
(3)sin$\frac{π}{12}$-$\sqrt{3}$cos$\frac{π}{12}$=2($\frac{1}{2}$sin$\frac{π}{12}$-$\frac{\sqrt{3}}{2}$cos$\frac{π}{12}$)=2(cos$\frac{π}{3}$sin$\frac{π}{12}$-sin$\frac{π}{3}$cos$\frac{π}{12}$)=2sin($\frac{π}{12}$-$\frac{π}{3}$)=-2sin$\frac{π}{4}$=-$\sqrt{2}$.
点评 本题考查了两角和与差的正弦公式,以及诱导公式,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
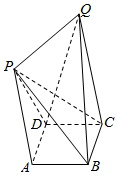 如图,在四棱锥P-ABCD中.底面ABCD为矩形,侧棱PA⊥平面ABCD,AP∥CQ,AB=2BC=2,CQ=$\frac{3}{2}$AP=3.
如图,在四棱锥P-ABCD中.底面ABCD为矩形,侧棱PA⊥平面ABCD,AP∥CQ,AB=2BC=2,CQ=$\frac{3}{2}$AP=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com