
设函数 ,
,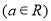 ;
; ,
, .
.
(1)求函数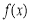 的单调区间;
的单调区间;
(2)当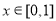 时,求函数
时,求函数 的最大值;
的最大值;
(3)求证:
(1)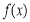 的定义域为
的定义域为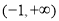 ,
,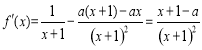 , 1分
, 1分
令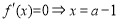 ,
,
ⅰ)当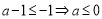 时:
时: 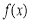 的增区间为
的增区间为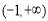 ;
;
ⅱ)当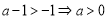 时:
时: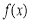 的减区间为
的减区间为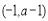 ;
;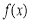 的增区间为
的增区间为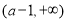 .
.
(2)当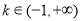 时,
时, 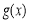 在
在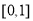 上的最大值为
上的最大值为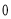 .
.
(3)见解析.
【解析】
试题分析:(1)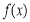 的定义域为
的定义域为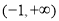 ,
,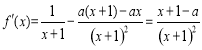 ,
,
分类讨论如下:
ⅰ)当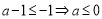 时:
时:
在区间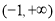 上,
上,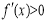 恒成立,故
恒成立,故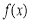 的增区间为
的增区间为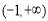 ;
;
ⅱ)当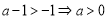 时:
时:
在区间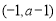 上,
上,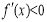 恒成立,故
恒成立,故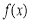 的减区间为
的减区间为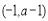 ;
;
在区间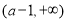 上,
上, 恒成立,故
恒成立,故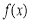 的增区间为
的增区间为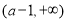 .
.
(2)令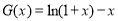 ,
,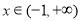 ,则
,则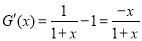 ,利用“表解法”确定函数的最值.
,利用“表解法”确定函数的最值.
表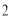 :
:
|
|
|
|
|
|
|
|
| 递减 | 极小值 | 递增 |
(3)由(1)可知:当a=1时,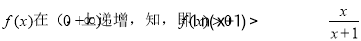
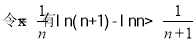 转化
转化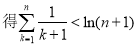
由(2)已证: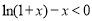
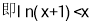
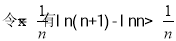
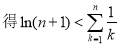 得证.
得证.
试题解析:(1)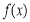 的定义域为
的定义域为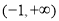 ,
,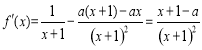 , 1分
, 1分
令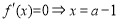 ,
,
ⅰ)当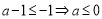 时:
时:
在区间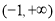 上,
上,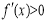 恒成立,故
恒成立,故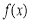 的增区间为
的增区间为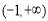 ; 2分
; 2分
ⅱ)当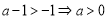 时:
时:
在区间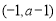 上,
上,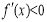 恒成立,故
恒成立,故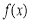 的减区间为
的减区间为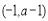 ; 3分
; 3分
在区间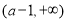 上,
上, 恒成立,故
恒成立,故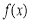 的增区间为
的增区间为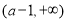 . 4分
. 4分
(2)ⅰ)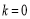 时,
时,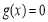 ,所以
,所以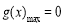 ; 5分
; 5分
ⅱ) 时,易知
时,易知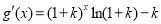 ,于是:
,于是: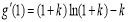 ,
,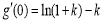 ,
,
由(1)可知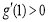 , 下证
, 下证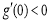 ,即证明不等式
,即证明不等式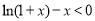 在
在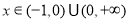 上恒成立.
上恒成立.
(法一)由上可知:不等式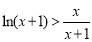 在
在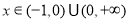 上恒成立,若
上恒成立,若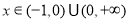 ,则
,则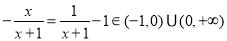 ,故
,故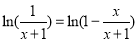
 ,即当
,即当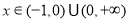 时,
时,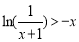 ,从而
,从而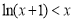 ,故当
,故当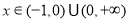 时,
时,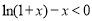 恒成立,即
恒成立,即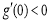 . 7分
. 7分
(法二)令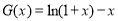 ,
,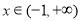 ,则
,则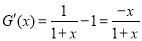 ,列表
,列表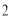 如下:
如下:
表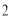 :
:
|
|
|
|
|
|
|
|
| 递减 | 极小值 | 递增 |
由表2可知:当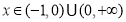 时,
时,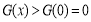 ,
,
故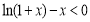 恒成立,即
恒成立,即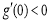 . 7分
. 7分
由于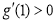 ,且
,且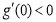 ,故函数
,故函数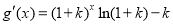 区间
区间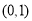 内必存在零点. 8分
内必存在零点. 8分
又当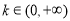 时,
时,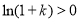 ,指数函数
,指数函数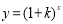 为增函数
为增函数 为增函数,
为增函数,
同理当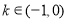 时,
时, ,指数函数
,指数函数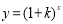 为减函数
为减函数 也为增函数,
也为增函数,
于是,当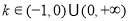 时,
时, 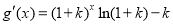 必为增函数,
必为增函数,
从而函数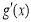 在区间
在区间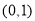 内必存在唯一零点,不妨记为
内必存在唯一零点,不妨记为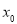 ,则
,则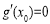 ,
,
易知当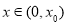 时,
时,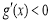 ,此时
,此时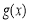 单调递减;
单调递减;
当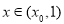 时,
时,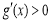 ,此时
,此时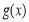 单调递增,
单调递增,
又易知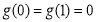 ,故
,故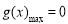 ;
;
综上,当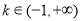 时,
时, 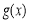 在
在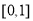 上的最大值为
上的最大值为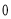 . 10分
. 10分
(3)由(1)可知:当a=1时,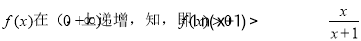
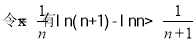
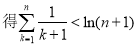 12分
12分
由(2)已证: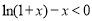
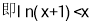
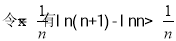
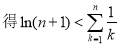
故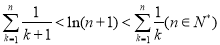 得证 14分
得证 14分
考点:1.应用导数研究函数的单调性;2.应用导数研究函数的单调性、极(最)值,3.应用导数证明不等式4.转化与化归思想.


科目:高中数学 来源:2015届广东省高三上学期暑假联考理科数学试卷(解析版) 题型:解答题
设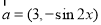 ,
, 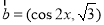 ,
,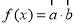
(1)求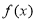 的最小正周期;
的最小正周期;
(2)求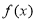 的最大值及取最大值时
的最大值及取最大值时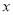 的集合;
的集合;
(3)求满足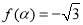 且
且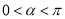 的角
的角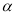 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2015届广东省广州市高三上学期第一次质量检测理科数学试卷(解析版) 题型:填空题
在平面直角坐标系中,倾斜角为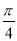 的直线
的直线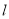 与曲线
与曲线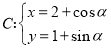 ,(
,(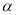 为参数)交于
为参数)交于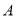 、
、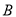 两点,且
两点,且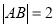 ,以坐标原点
,以坐标原点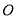 为极点,
为极点, 轴正半轴为极轴建立极坐标系,则直线
轴正半轴为极轴建立极坐标系,则直线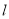 的极坐标方程是________.
的极坐标方程是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com