
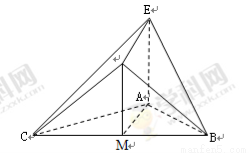
在如图所示的几何体中,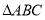 是边长为
是边长为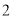 的正三角形,
的正三角形,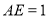 ,
,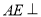 平面
平面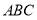 ,平面
,平面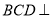 平面
平面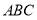 ,
,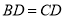 ,且
,且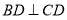 .
.
(1)证明: //平面
//平面 ;
;
(2)证明:平面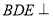 平面
平面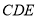 ;
;
(3)求该几何体的体积.
(1)详见解析;(2)详见解析;(3)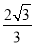
【解析】
试题分析:(1)取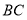 的中点
的中点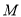 ,根据等腰三角形中线即为高线可得
,根据等腰三角形中线即为高线可得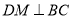 ,又因为面
,又因为面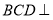 平面
平面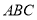 ,根据面面垂直的性质定理可得
,根据面面垂直的性质定理可得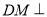 平面
平面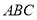 ,已知
,已知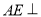 平面
平面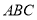 ,所以
,所以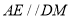 ,根据线面平行的判定定理可得
,根据线面平行的判定定理可得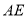 //平面
//平面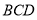 。(2)因为
。(2)因为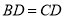 ,且
,且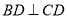 ,斜边中线
,斜边中线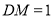 ,又因为
,又因为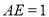 ,
,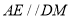 可证得
可证得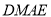 是平行四边形,可得
是平行四边形,可得 ,根据线面垂直的判定定理可证得
,根据线面垂直的判定定理可证得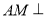 平面
平面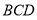 ,即
,即 平面
平面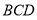 ,从而可得
,从而可得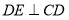 ,又因为
,又因为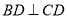 即可证得
即可证得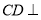 平面
平面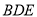 ,从而证得平面
,从而证得平面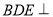 平面
平面 。(3)根据前两问的条件可证得
。(3)根据前两问的条件可证得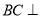 平面
平面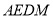 ,从而可将此几何体分割为以四边形
,从而可将此几何体分割为以四边形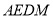 为底面的两个四棱锥,然后再求其体积。
为底面的两个四棱锥,然后再求其体积。
试题解析:证明:
(1) 取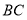 的中点
的中点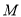 ,连接
,连接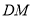 、
、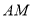 ,
,
由已知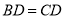 ,可得:
,可得: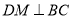 ,
,
又因为平面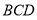 ⊥平面
⊥平面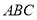 ,平面
,平面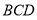
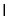 平面
平面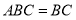 ,
,
所以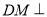 平面
平面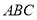 ,
,
因为 平面
平面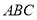 , 所以
, 所以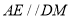 ,
,
又因为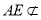 平面
平面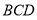 ,
,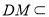 平面
平面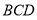 ,
,
所以 平面
平面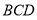 . 4分
. 4分
(2)由(1)知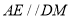 ,又
,又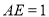 ,
,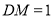 ,
,
所以四边形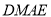 是平行四边形,则有
是平行四边形,则有 ,
,
由(1)得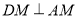 ,又
,又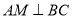 ,
,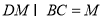

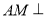 平面
平面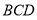 , 所以
, 所以 平面
平面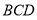 ,
,
又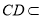 平面
平面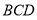 ,所以
,所以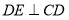 ,
,
由已知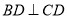 ,
, 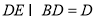 ,
,
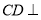 平面
平面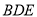 ,
,
因为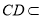 平面
平面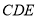 , 所以平面
, 所以平面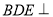 平面
平面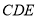 . 10分
. 10分
(也可利用勾股定理等证明题中的垂直关系)
(3)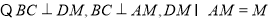 ,
,
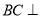 平面
平面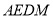 , 11分
, 11分
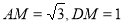 ,易得四边形
,易得四边形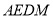 为矩形其面积
为矩形其面积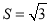 , 12分
, 12分
故该几何体的体积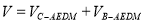 =
=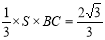 . 14分
. 14分
考点:1线面平行;2面面垂直;3棱锥的体积。


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源:2015届广东阳东广雅、阳春实验中学高二上期末文数学卷(解析版) 题型:选择题
公比为2的等比数列 的各项都是正数,且
的各项都是正数,且 =16,则
=16,则 =( ).
=( ).
A.1 B.2 C.4 D.8
查看答案和解析>>
科目:高中数学 来源:2015届广东省等七校高二2月联考理科数学试卷(解析版) 题型:选择题
下列说法正确的是( )
A.命题“若 ,则
,则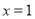 ”的否命题为:“若
”的否命题为:“若 ,则
,则 ”
”
B.若命题 ,则命题
,则命题
C.命题“若 ,则
,则 ”的逆否命题为真命题
”的逆否命题为真命题
D.“ ”是“
”是“ ”的必要不充分条件
”的必要不充分条件
查看答案和解析>>
科目:高中数学 来源:2015届广东省等七校高二2月联考文科数学试卷(解析版) 题型:填空题
设抛物线 ,过焦点
,过焦点 的直线交抛物线于
的直线交抛物线于 两点,线段
两点,线段 的中点的横坐标为
的中点的横坐标为 ,
,
则 =_____________.
=_____________.
查看答案和解析>>
科目:高中数学 来源:2015届广东省等七校高二2月联考文科数学试卷(解析版) 题型:选择题
如右图所示,一个空间几何体的主视图和左视图都是边长为 的正方形,俯视图是一个直径为
的正方形,俯视图是一个直径为 的圆,那么这个几何体的全面积为( )
的圆,那么这个几何体的全面积为( )

A. B.
B. C.
C. D.
D. 
查看答案和解析>>
科目:高中数学 来源:2015届广东汕头金山中学高二上学期期末理科数学试卷(解析版) 题型:选择题
已知圆锥的底面半径为 ,高为
,高为 ,在它的所有内接圆柱中,全面积的最大值为( )
,在它的所有内接圆柱中,全面积的最大值为( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2015届广东惠州高二第一学期期末考试理科数学试卷(解析版) 题型:选择题
已知椭圆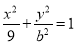
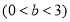 ,左右焦点分别为
,左右焦点分别为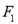 ,
,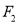 ,过
,过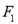 的直线交椭圆于
的直线交椭圆于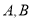 两点,若
两点,若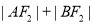 的最大值为8,则
的最大值为8,则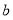 的值是( )
的值是( )
A.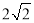 B.
B.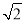 C.
C.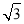 D.
D.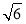
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com