
| A. | -2f′(1) | B. | $\frac{1}{2}$f′(1) | C. | -$\frac{1}{2}$f′(1) | D. | f($\frac{1}{2}$) |
分析 直接根据导数定义$\underset{lim}{△x→0}$$\frac{f(1-2△x)-f(1)}{△x}$=-2f'(x),即可得出结果.
解答 解:根据导数的定义,
f'(1)=$\underset{lim}{△x→0}$$\frac{f(1-2△x)-f(1)}{(1-2△x)-1}$
=$\underset{lim}{△x→0}$[$\frac{f(1-2△x)-f(1)}{△x}$•(-$\frac{1}{2}$)]
=-$\frac{1}{2}$•$\underset{lim}{△x→0}$$\frac{f(1-2△x)-f(1)}{△x}$,
所以,$\underset{lim}{△x→0}$$\frac{f(1-2△x)-f(1)}{△x}$=-2f'(1),
即原式=-2f'(1),
故答案为:A.
点评 本题主要考查了导数的定义和极限的运算,进行合理的恒等变形是解决问题的关键,属于基础题.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳八中高三上学期月考二数学(文)试卷(解析版) 题型:填空题
函数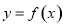 图象上不同两点
图象上不同两点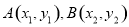 处的切线的斜率分别是
处的切线的斜率分别是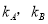 ,规定
,规定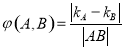 (
(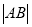 为线段AB的长度)叫做曲线
为线段AB的长度)叫做曲线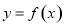 在点A与点B之间的“弯曲度”,给出以下命题:
在点A与点B之间的“弯曲度”,给出以下命题:
①函数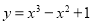 图象上两点A与B的横坐标分别为1和2,则
图象上两点A与B的横坐标分别为1和2,则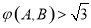 ;
;
②存在这样的函数,图象上任意两点之间的“弯曲度”为常数;
③设点A,B是抛物线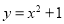 上不同的两点,则
上不同的两点,则 ;
;
④设曲线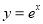 (e是自然对数的底数)上不同两点
(e是自然对数的底数)上不同两点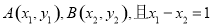 ,若
,若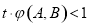 恒成立,则实数t的取值范围是
恒成立,则实数t的取值范围是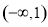 .
.
其中真命题的序号为________.(将所有真命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com