
【题目】已知抛物线![]() :
:![]() 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.

(1)求抛物线![]() 的方程;
的方程;
(2)设直线![]() 与抛物线
与抛物线![]() 交于两点
交于两点![]() 、
、![]() ,且
,且![]() ,
,![]() 是弦
是弦![]() 中点,过
中点,过![]() 作平行于
作平行于![]() 轴的直线交抛物线
轴的直线交抛物线![]() 于点
于点![]() ,得到
,得到![]() ,再分别过弦
,再分别过弦![]() 、
、![]() 的中点作平行于
的中点作平行于![]() 轴的直线依次交抛物线
轴的直线依次交抛物线![]() 于点
于点![]() 、
、![]() ,得到
,得到![]() 和
和![]() ,按此方法继续下去,解决下列问题:
,按此方法继续下去,解决下列问题:
①求证:![]() ;
;
②计算![]() 的面积
的面积![]() ;
;
③根据![]() 的面积
的面积![]() 的计算结果,写出
的计算结果,写出![]() 、
、![]() 的面积,请设计一种求抛物线
的面积,请设计一种求抛物线![]() 与线段
与线段![]() 所围成封闭图形面积的方法,并求此封闭图形的面积.
所围成封闭图形面积的方法,并求此封闭图形的面积.
【答案】(1)![]() ;(2)①见解析; ②
;(2)①见解析; ②![]() ;③
;③![]() ,无穷等比数列各项和.
,无穷等比数列各项和.![]() .
.
【解析】
(1)由抛物线的定义、结合已知可以直接求出![]() 的值,进而可以求出抛物线的方程;
的值,进而可以求出抛物线的方程;
(2)①:直线方程与抛物线方程联立,根据根的判别式、根与系数的关系、结合
![]() ,可以证明出
,可以证明出![]() ;
;
②:利用中点坐标公式和三角形面积公式直接求解即可;
③:同②可知:![]() 只与
只与![]() 有关,于是可知
有关,于是可知![]() ,
,![]() 分别与
分别与![]() 、
、![]() 有关,这样可以求出它们的面积;这样无限操作下去,每次得到的三角形面积都相等,面积是一个等比数列,每次得到的三角形的个数也是等比数列,利用无穷等比数列前
有关,这样可以求出它们的面积;这样无限操作下去,每次得到的三角形面积都相等,面积是一个等比数列,每次得到的三角形的个数也是等比数列,利用无穷等比数列前![]() 项和公式,这样可以求出抛物线
项和公式,这样可以求出抛物线![]() 与线段
与线段![]() 所围成封闭图形面积.
所围成封闭图形面积.
(1)抛物线的准线方程为:![]() ,由抛物线的定义可知:
,由抛物线的定义可知:![]() ,所以抛物线的方程为:
,所以抛物线的方程为:![]() ;
;
(2)①:联立直线和抛物线方程得: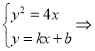
![]()
![]() ,
,
∴![]() ,
,![]() ;
;
∴![]()
![]() ;
;
②:由中点坐标公式可得:![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,
,![]() ;
;
③:由同②可知:![]() 只与
只与![]() 有关,而
有关,而![]()
![]() ,
,
所以![]() ,这样无限操作下去,第
,这样无限操作下去,第![]() 次操作,得到
次操作,得到![]() 个小三角形,每个三角形的面积为:
个小三角形,每个三角形的面积为:![]() ,这无穷多个三角形的面积之和就是抛物线
,这无穷多个三角形的面积之和就是抛物线![]() 与线段
与线段![]() 所围成封闭图形面积,所以有
所围成封闭图形面积,所以有
![]()
![]()
所求的面积为![]() .
.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】2002年在北京召开的国际数学家大会的会标是以我国古代数学家的弦图为基础设计的.弦图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形(如图).设其中直角三角形中较小的锐角为![]() ,且
,且![]() ,如果在弦图内随机抛掷1000米黑芝麻(大小差别忽略不计),则落在小正方形内的黑芝麻数大约为( )
,如果在弦图内随机抛掷1000米黑芝麻(大小差别忽略不计),则落在小正方形内的黑芝麻数大约为( )
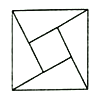
A. 350B. 300C. 250D. 200
查看答案和解析>>
科目:高中数学 来源: 题型:
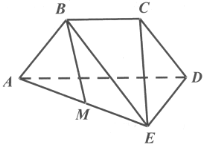
【题目】如图等腰梯形![]() 中
中![]() ,且平面
,且平面 ![]() 平面
平面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求证:平面 ![]() 平面
平面![]() ;
;
(3)若二面角![]() 的大小为
的大小为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某地区2008年至2014年中,每年的居民人均纯收入y(单位:千元)的数据如下表:
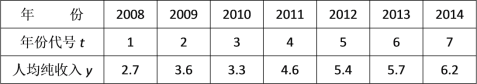
对变量t与y进行相关性检验,得知t与y之间具有线性相关关系.
(1)求y关于t的线性回归方程;
(2)预测该地区2016年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
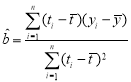 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加某次知识竞赛测试得学生中随机抽取60名学生,将其成绩(百分制均为整数)分成6段![]() ,
,![]() ,…,
,…,![]() 后得到如下部分频率直方分布图,观察图形得信息,回答下列问题:
后得到如下部分频率直方分布图,观察图形得信息,回答下列问题:
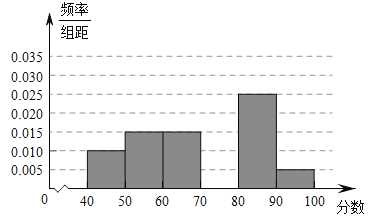
(1)求分数在![]() 内的频率;
内的频率;
(2)若用样本估计总体,已知该校参加知识竞赛一共有300人,请估计本次考试成绩不低于80分的人数;
(3)统计方法中,同一组数据常用该组区间中点值作为代表,据此估计本次考试的平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 处的切线
处的切线![]() 与直线
与直线![]() 平行.
平行.
(1)求实数![]() 的值;
的值;
(2)若函数![]() 在
在![]() 上恰有两个零点,求实数
上恰有两个零点,求实数![]() 的取值范围.
的取值范围.
(3)记函数![]() ,设
,设![]() 是函数
是函数![]() 的两个极值点,若
的两个极值点,若![]() ,且
,且![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com