Question

【题目】已知圆，过原点的直线与其交于不同的两点.

（1）求直线斜率的取值范围；

（2）求线段的中点的轨迹的方程；

（3）若直线与曲线只有一个公共点，求的取值范围.

Answer 1

【答案】(1) ；（2）；（3）或.

【解析】

试题分析：（1）直线与其交于不同的两点，，可得，即可求直线斜率的取值范围；（2）利用，即可求线段的中点的轨迹的方程；（3）利用直线与曲线只有一个公共点，分类讨论，即可求的取值范围.

试题解析：（1）由得

直线过原点，可设其方程：

∵直线与其将于不同的两点∴∴

（2）设点，∵点为线段的中点，

而曲线是圆心为，半径的圆，∴

∴（且）化简得①

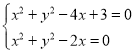由得

是不同的两点，且点的坐标满足①

因此点满足②

这是圆心为，半径为的一段圆弧（不包括端点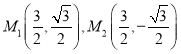），反之，可验证以方程②的解为坐标的点是曲线上的一个点，因此②是轨迹的方程.

（3）设直线过

设直线与圆相切于点，则有，解得

直线的斜率为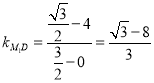

类似的可得

综上，若直线与曲线只有一个公共点，

则的取值范围是或.