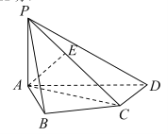
【题目】如图，在四棱锥
中，
底面
是
的中点.
（1）证明：
平面
；
（2）求
和平面
所成的角的正切值.
【答案】（1）证明见解析；（2）
.
【解析】
试题分析：（1）由
为等边三角形可得
，于是
，通过证明
平面
得出
，故而
平面
；（2）取
中点
，连接
，则可证明
平面
，故
为
与平面
所成的角，利用勾股定理求出
，
即可得出
.
试题解析：（1）∵在
中，
，
∴
为等边三角形，∴
…………（1分）
∵在
中，
是
的中点，∴
∵
与
为平面
内两条相交直线，∴
平面
…………（4分）
∵
平面
，∴
∵
与
为平面
内两条相交直线，∴
平面
…………（6分）
（2）取
中点
，连接
、
，设
∵在
中，
为
中点，∴
∵
底面
底面
，∴
∵
与
为平面
内两条相交直线，∴
平面
∴
为
在平面
内的射影，∴
为
和平面
所成的角…………（9分）
∵
底面
底面
，∴
∵
，∴
∴在
中，
∴
和平面
所成的角的正切值为…………（12分）
科目：高中数学 来源： 题型：
【题目】如图，已知圆
，点
，
是圆
上任意一点，线段
的垂直平分线和半径
相交于
.
（1）求动点
的轨迹
的方程；
（2）设直线
与（Ⅰ）中轨迹相交于
，
两点，直线
，，
的斜率分别为
，
，
（其中
），
的面积为
，以，为直径的圆的面积分别为
，
，若，，恰好构成等比数列，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】以下有五个步骤:①拨号；②提起话筒(或免提功能)；③开始通话或挂机(线路不通)；④等复话方信号；⑤结束通话.试写出一个打本地电话的算法________.(只写编号)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆
，过原点的直线
与其交于不同的两点
.
（1）求直线
斜率
的取值范围；
（2）求线段
的中点
的轨迹
的方程；
（3）若直线
与曲线
只有一个公共点，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥P－ABCD的底面ABCD为直角梯形，其中BA⊥AD，CD⊥AD，CD＝AD＝2AB，PA⊥底面ABCD，E是PC的中点．
（1）求证：BE∥平面PAD；
（2）若AP＝2AB，求证：BE⊥平面PCD．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列关于框图的逻辑结构的说法正确的是
A. 条件结构中不含有顺序结构
B. 用顺序结构画出的电水壶烧开水的框图是唯一的
C. 条件结构中一定有循环结构
D. 循环结构中一定包含条件结构
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1，已知四边形
为直角梯形，
，
，
，
为等边三角形，
，
，如图2，将
，
分别沿
折起，使得平面
平面
，平面
平面，连接
，设
为
上任意一点．
（1）证明：
平面
；
（2）若
，求
的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
