
【题目】如图,已知圆![]() ,点
,点![]() ,
,![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线和半径
的垂直平分线和半径![]() 相交于
相交于![]() .
.

(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设直线![]() 与(Ⅰ)中轨迹
与(Ⅰ)中轨迹![]() 相交于
相交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() (其中
(其中![]() ),
),![]() 的面积为
的面积为![]() ,以
,以![]() ,
,![]() 为直径的圆的面积分别为
为直径的圆的面积分别为![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() 恰好构成等比数列,求
恰好构成等比数列,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)连接![]() ,根据题意,
,根据题意,![]() ,可得
,可得![]() ,故动点
,故动点![]() 的轨迹
的轨迹![]() 是以
是以![]() ,
,![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆.解出即可;(2)设直线
的椭圆.解出即可;(2)设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() .与椭圆的方程联立可得
.与椭圆的方程联立可得![]() ,利用根与系数的关系及其
,利用根与系数的关系及其![]() ,
,![]() ,
,![]() 构成等比数列,可得
构成等比数列,可得![]() ,解得
,解得![]() ,
,![]() .利用
.利用![]() ,解得
,解得![]() ,且
,且![]() .利用
.利用![]()
![]() ,可得
,可得![]() 为定值.代入利用基本不等式的性质即可得出
为定值.代入利用基本不等式的性质即可得出![]() 的取值范围.
的取值范围.
试题解析:(1)连接![]() ,根据题意,
,根据题意,![]() ,则
,则![]() ,
,
故动点![]() 的轨迹
的轨迹![]() 是以
是以![]() ,
,![]() 为焦点,长轴长为4的椭圆.
为焦点,长轴长为4的椭圆.
设其方程为![]() ,可知
,可知![]() ,
,![]() ,则
,则![]() ,
,
∴点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() .
.
联立 ,化为
,化为![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,![]() 构成等比数列,∴
构成等比数列,∴![]() ,化为
,化为![]() ,
,
∴![]() ,解得
,解得![]() .∵
.∵![]() ,∴
,∴![]() .
.
此时![]() ,解得
,解得![]() .
.
又由![]() 、
、![]() 、
、![]() 三点不共线得
三点不共线得![]() ,从而
,从而![]() .
.
故![]() ,
,
又![]() ,则
,则![]()
![]() 为定值.
为定值.
∴![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
综上:![]() .
.


科目:高中数学 来源: 题型:
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如下图.
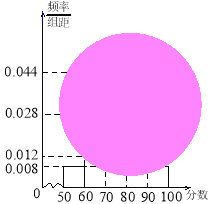

(1)求分数在![]() 的频率及全班人数;
的频率及全班人数;
(2)求分数在![]() 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中![]() 间矩形的高;
间矩形的高;
(3)若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
喜欢 | 不喜欢 | 合计 | |
大于40岁 | 20 | 5 | 25 |
20岁至40岁 | 10 | 20 | 30 |
合计 | 30 | 25 | 55 |
(1)判断是否有99.5%的把握认为喜欢“人文景观”景点与年龄有关?
(2)用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,建立平面直角坐标系![]() ,
,![]() 轴在地平面上,
轴在地平面上,![]() 轴垂直于地平面,单位长度为1千米,某炮位于坐标原点,已知炮弹发射后的轨迹在方程
轴垂直于地平面,单位长度为1千米,某炮位于坐标原点,已知炮弹发射后的轨迹在方程![]() 表示的曲线上,其中
表示的曲线上,其中![]() 与发射方向有关,炮的射程是指炮弹落地点的横坐标.
与发射方向有关,炮的射程是指炮弹落地点的横坐标.

(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标![]() 不超过多少时,炮弹可以击中它?请说明理由.
不超过多少时,炮弹可以击中它?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若大前提是:所有边长都相等的凸多边形是正多边形,小前提是:菱形是所有边长都相等的凸多边形,结论是:菱形是正多边形,那么这个演绎推理出错在( )
A. 大前提出错 B. 小前提出错 C. 推理过程出错 D. 没有出错
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若不等式x2-(a+1)x+a≤0的解集是[-4,3]的子集,则a的取值范围是( )
A. [-4,1] B. [-4,3] C. [1,3] D. [-1,3]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com