[题目]已知边长为的正三角形三个顶点都在球的表面上.且球心到平面的距离为该球半径的一半.则球的表面积为题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知边长为的正三角形三个顶点都在球的表面上，且球心到平面的距离为该球半径的一半，则球的表面积为___________

【答案】

【解析】

如图,设OO′⊥平面ABC,垂足是O′，设球半径为r，

∵边长为的正三角形ABC三个顶点都在球O的表面上，

且球心O到平面ABC的距离为该球半径的一半，

∴，

∵

解得，

∴球O的表面积

故答案为： .

点睛:本题考查的是空间几何体与球接、切问题.这种问题的求解方法:(1)求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．

(2)若球面上四点构成的三条线段两两互相垂直，且，一般把有关元素“补形”成为一个球内接长方体，利用求解．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，正方体的棱长为1，分别是棱的中点，过的平面与棱分别交于点 .设，．

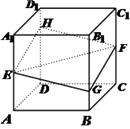
①四边形一定是菱形；② 平面；③四边形的面积在区间上具有单调性；④四棱锥的体积为定值.
以上结论正确的个数是（）
A.4
B.3
C.2
D.1

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f(x)＝2x－的定义域为(0，1](a为实数).
（1）当a＝1时，求函数y＝f(x)的值域；
（2）求函数y＝f(x)在区间(0，1]上的最大值及最小值，并求出当函数f(x)取得最值时x的值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数，给出以下四个命题：
① ，有；
② 且，有；
③ ，有；
④ ， .
其中所有真命题的序号是（）
A.①②
B.③④
C.①②③
D.①②③④

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数 .
（I）若曲线存在斜率为-1的切线，求实数a的取值范围；
（II）求的单调区间；
（III）设函数，求证：当时，在上存在极小值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在四棱锥中，底面为平行四边形，，，，点在底面内的射影在线段上，且，，为的中点，在线段上，且．

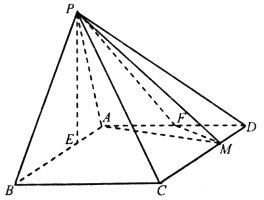
（Ⅰ）当时，证明：平面平面；

（Ⅱ）当平面与平面所成的二面角的正弦值为时，求四棱锥的体积．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数（）.

(1)若，求函数的极大值；

(2)若时，恒有成立，求实数的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在小明的婚礼上，为了活跃气氛，主持人邀请10位客人做一个游戏.第一轮游戏中，主持人将标有数字1,2，…，10的十张相同的卡片放入一个不透明箱子中，让客人依次去摸，摸到数字6,7，…，10的客人留下，其余的淘汰，第二轮放入1,2，…，5五张卡片，让留下的客人依次去摸，摸到数字3,4,5的客人留下，第三轮放入1,2,3三张卡片，让留下的客人依次去摸，摸到数字2,3的客人留下，同样第四轮淘汰一位，最后留下的客人获得小明准备的礼物.已知客人甲参加了该游戏.

（1）求甲拿到礼物的概率；

（2）设表示甲参加游戏的轮数，求的概率分布和数学期望.