
分析 设直线MN方程为:x=my+2,由 $\left\{\begin{array}{l}{x=my+2}\\{{x}^{2}+3{y}^{2}=6}\end{array}\right.$得(m2+3)y2+4my-2=0,可得△MNA的面积s=$\frac{1}{2}×AF×$|y1-y2|=3$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{6\sqrt{6}\sqrt{{m}^{2}+1}}{{m}^{2}+3}=\frac{6\sqrt{6}\sqrt{{m}^{2}+1}}{{m}^{2}+1+2}$=$\frac{6\sqrt{6}}{\sqrt{{m}^{2}+1}+\frac{2}{\sqrt{{m}^{2}+1}}}$$≤\frac{6\sqrt{6}}{2\sqrt{2}}=3\sqrt{3}$
解答 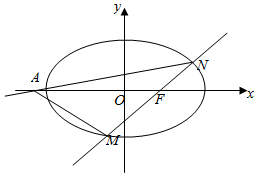 解:∵椭圆C:x2+3y2=6的右焦点为(2,0),故设直线MN方程为:x=my+2,
解:∵椭圆C:x2+3y2=6的右焦点为(2,0),故设直线MN方程为:x=my+2,
由 $\left\{\begin{array}{l}{x=my+2}\\{{x}^{2}+3{y}^{2}=6}\end{array}\right.$得(m2+3)y2+4my-2=0,
${y}_{1}+{y}_{2}=\frac{-4m}{{m}^{2}+3}$,${y}_{1}{y}_{2}=\frac{-2}{{m}^{2}+3}$,
,△MNA的面积s=$\frac{1}{2}×AF×$|y1-y2|=3$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{6\sqrt{6}\sqrt{{m}^{2}+1}}{{m}^{2}+3}=\frac{6\sqrt{6}\sqrt{{m}^{2}+1}}{{m}^{2}+1+2}$=$\frac{6\sqrt{6}}{\sqrt{{m}^{2}+1}+\frac{2}{\sqrt{{m}^{2}+1}}}$$≤\frac{6\sqrt{6}}{2\sqrt{2}}=3\sqrt{3}$,
当m=±1时,△MNA的面积的有最大值为3$\sqrt{3}$,
故答案为:3$\sqrt{3}$.
点评 本题考查了椭圆与直线的位置关系,三角形面积计算,属于中档题.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:解答题
 如图,曲线Γ由曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和曲线C2::$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0,y≤0)组成,其中点F1,F2为曲线C1所在圆锥曲线的焦点,点F3,F4为曲线C2所在圆锥曲线的焦点,已知F2(2,0)F4(6,0).
如图,曲线Γ由曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和曲线C2::$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0,y≤0)组成,其中点F1,F2为曲线C1所在圆锥曲线的焦点,点F3,F4为曲线C2所在圆锥曲线的焦点,已知F2(2,0)F4(6,0).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{a^2}{2}$ | B. | $\frac{{\sqrt{6}}}{4}{a^2}$ | C. | $\frac{{\sqrt{3}}}{4}{a^2}$ | D. | $\frac{{\sqrt{3}}}{2}{a^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | E(η)=5,D(ξ)=3 | B. | E(η)=3,D(ξ)=27 | C. | E(η)=9,D(ξ)=81 | D. | E(η)=5,D(ξ)=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某工厂为制定下一阶段生产某种产品的方案,工厂技术部门开展了两项统计,其一是对该厂48名师傅生产的产品精度情况进行了调查,得到如下的2×2列联表1(单位:个);其二是对某师傅加工零件个数n1(单位:个)和加工时间t1(单位:小时,i-1,2,…6)作了6次试验,并对获得的数据作了初步处理,得到下面的散点图及一些统计量的值如表2.
某工厂为制定下一阶段生产某种产品的方案,工厂技术部门开展了两项统计,其一是对该厂48名师傅生产的产品精度情况进行了调查,得到如下的2×2列联表1(单位:个);其二是对某师傅加工零件个数n1(单位:个)和加工时间t1(单位:小时,i-1,2,…6)作了6次试验,并对获得的数据作了初步处理,得到下面的散点图及一些统计量的值如表2.| 类别 | 达到精品级 | 未达到精品级 | 总计 |
| 高级技工 | 22 | 6 | 28 |
| 中级技工 | 10 | 10 | 20 |
| 总计 | 32 | 16 | 48 |
| $\overline{n}$=$\frac{1}{6}$$\sum_{i=1}^{6}{n}_{i}$ | $\overline{t}$=$\frac{1}{6}$$\sum_{i=1}^{6}{t}_{i}$ | $\sum_{i=1}^{6}{n}_{i}$ 2 | $\sum_{i=1}^{6}{t}_{i}$ 2 | $\sum_{i=1}^{6}{n}_{i}{t}_{i}$ | $\sum_{i=1}^{6}$(ni-$\overline{n}$)2 | $\sum_{i=1}^{6}$(ti-$\overline{t}$)2 | $\sum_{i=1}^{6}$(ni-$\overline{n}$)(ti-$\overline{t}$) |
| 4.5 | 4.125 | 139 | 109.562 | 112.75 | 17.5 | 7.468 | 11.375 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,$\overrightarrow{DQ}$=λ$\overrightarrow{DC}$,$\overrightarrow{CP}$=(1-λ)$\overrightarrow{CB}$,则$\overrightarrow{AP}$•$\overrightarrow{AQ}$的取值范围是( )
如图,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,$\overrightarrow{DQ}$=λ$\overrightarrow{DC}$,$\overrightarrow{CP}$=(1-λ)$\overrightarrow{CB}$,则$\overrightarrow{AP}$•$\overrightarrow{AQ}$的取值范围是( )| A. | (-∞,$\frac{9}{4}$] | B. | [0,2] | C. | [0,3] | D. | [0,$\frac{9}{4}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com