
| A. | $\frac{a^2}{2}$ | B. | $\frac{{\sqrt{6}}}{4}{a^2}$ | C. | $\frac{{\sqrt{3}}}{4}{a^2}$ | D. | $\frac{{\sqrt{3}}}{2}{a^2}$ |
分析 如图连结AC交BD与O,连结OE,由OE∥AC1,得AC1∥平面BDE,求出△BDE的面积即可.
解答 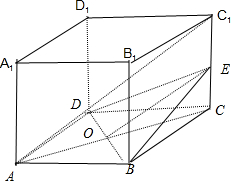 解:如图连结AC交BD与O,连结OE,
解:如图连结AC交BD与O,连结OE,
因为O、E分别是AC、CC1的中点,
∴OE∥AC1,
又因为OE?平面BDE,AC1?平面BDE.
∴AC1∥平面BDE,∴△DBE就是过BD且与直线AC1平行的截面.
易得△DBE是等腰△,且DB⊥OE
在△DBE中,BD=$\sqrt{2}a$,OE=$\sqrt{O{C}^{2}+C{E}^{2}}=\frac{\sqrt{3}}{2}a$
∴${S}_{△DBE}=\frac{1}{2}×DB×OE=\frac{1}{2}×\sqrt{2}a×$$\frac{\sqrt{3}}{2}a$=$\frac{\sqrt{6}}{4}{a}^{2}$.
故选:B.
点评 本题考查了线线垂直、线面平行的判定,属于基础题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $6+2\sqrt{3}$ | B. | $7+2\sqrt{3}$ | C. | $6+4\sqrt{3}$ | D. | $7+4\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为${F_1}{、_{_1}}{F_2}$,点B是双曲线的右顶点,A是其虚轴的端点,如图所示.若${S_{△AB{F_2}}}=\frac{1}{4}{S_{△AOB}}$,则双曲线的两条渐近线的夹角(锐角或直角)的正切值为( )
已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为${F_1}{、_{_1}}{F_2}$,点B是双曲线的右顶点,A是其虚轴的端点,如图所示.若${S_{△AB{F_2}}}=\frac{1}{4}{S_{△AOB}}$,则双曲线的两条渐近线的夹角(锐角或直角)的正切值为( )| A. | $\frac{5}{4}$ | B. | $\frac{24}{7}$ | C. | $-\frac{21}{24}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | c<a<b | C. | b<c<a | D. | a<c<b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com