
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
分析 (1)根据特称命题的否定是全称命题进行判断
(2)根据逆否命题的等价性以及充分条件和必要条件的定义进行判断
(3)根据充分条件和必要条件的定义进行判断.
解答 解:(1)命题“?x0∈R,x02+|x0|<0”的否定是“?x∈R,x2+|x|≥0”;正确,为真命题.
(2)若p是q的必要条件,则¬q是¬p必要条件,即¬p是¬q的充分条件;正确,为真命题,
(3)当a>b时,($\frac{3}{4}$)a>($\frac{3}{4}$)b,不成立,
反之当($\frac{3}{4}$)a>($\frac{3}{4}$)b时,a>b也不成立,
则a>b是($\frac{3}{4}$)a>($\frac{3}{4}$)b的既不充分也不必要条件.故(3)错误,
故正确的是(1)(2),
故选:B
点评 本题主要考查命题的真假判断,涉及含有量词的命题的否定,充分条件和必要条件的判断,综合性较强,但难度不大.


科目:高中数学 来源: 题型:解答题
| X | 1 | 2 | … | n | … |
| P | $\frac{1}{2}$ | $\frac{1}{{2}^{2}}$ | … | $\frac{1}{{2}^{n}}$ | … |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 合格品数 | 次品数 | 总数 | |
| 第一台加工数 | 45 | 10 | 55 |
| 第二台加工数 | 40 | 5 | 45 |
| 总计 | 85 | 15 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15种 | B. | 30种 | C. | 90种 | D. | 180种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
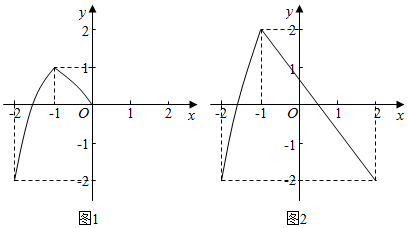
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com