
【题目】过抛物线![]() 焦点的直线
焦点的直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,与圆
两点,与圆![]() 交于
交于![]() ,
,![]() 两点,若有三条直线满足
两点,若有三条直线满足![]() ,则
,则![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】分析:(1)当直线![]() 与
与![]() 轴垂直时,满足
轴垂直时,满足![]() ;
;
(2)当直线![]() 不与
不与![]() 轴垂直时,直线
轴垂直时,直线![]() 方程
方程![]() .四点位置分两种情况:
.四点位置分两种情况:
①四点顺序为![]() ,AB的中点为(1,0),这样的直线不存在;
,AB的中点为(1,0),这样的直线不存在;
②四点顺序为![]() 时,得
时,得![]() ,即焦点弦长等于圆的直径,设
,即焦点弦长等于圆的直径,设![]() ,联立直线
,联立直线![]() 与抛物线方程,由韦达定理
与抛物线方程,由韦达定理![]() ,则
,则![]() ,又
,又![]() ,所以
,所以![]() ,继而得
,继而得![]() 时有两条满足条件的直线,从而得到答案.
时有两条满足条件的直线,从而得到答案.
详解:(1)当直线![]() 轴时,直线
轴时,直线![]() :
:![]() 与抛物线交于
与抛物线交于![]() ,与圆
,与圆![]() 交于
交于![]() ,满足
,满足![]() .
.
(2)当直线![]() 不与
不与![]() 轴垂直时,设直线
轴垂直时,设直线![]() 方程
方程![]() .
.![]()
联立方程组![]() 化简得
化简得![]()
由韦达定理 ![]()
由抛物线得定义,过焦点F的线段![]()
当四点顺序为![]() 时
时
![]()
![]() AB的中点为焦点F(1,0),这样的不与
AB的中点为焦点F(1,0),这样的不与![]() 轴垂直的直线不存在;
轴垂直的直线不存在;
当四点顺序为![]() 时,
时,
![]()
![]()
![]()
又![]() ,
,
![]() ,即
,即![]()
当![]() 时存在互为相反数的两斜率k,即存在关于
时存在互为相反数的两斜率k,即存在关于![]() 对称的两条直线。
对称的两条直线。
综上,当![]() 时有三条满足条件的直线.
时有三条满足条件的直线.
故选B.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 是平行四边形
是平行四边形![]() 所在平面外一点,如果
所在平面外一点,如果![]() ,
,![]() ,
,![]() .(1)求证:
.(1)求证:![]() 是平面
是平面![]() 的法向量;
的法向量;
(2)求平行四边形![]() 的面积.
的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:
(1)由题意结合空间向量数量积的运算法则计算可得![]() ,
,![]() .则
.则![]() ,
,![]() ,结合线面垂直的判断定理可得
,结合线面垂直的判断定理可得![]() 平面
平面![]() ,即
,即![]() 是平面
是平面![]() 的法向量.
的法向量.
(2)利用平面向量的坐标计算可得![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
试题解析:
(1)∵![]() ,
,
![]() .
.
∴![]() ,
,![]() ,又
,又![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() 是平面
是平面![]() 的法向量.
的法向量.
(2)∵![]()
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故![]() ,
,![]()
![]() .
.
【题型】解答题
【结束】
19
【题目】(1)求圆心在直线![]() 上,且与直线
上,且与直线![]() 相切于点
相切于点![]() 的圆的方程;
的圆的方程;
(2)求与圆![]() 外切于点
外切于点![]() 且半径为
且半径为![]() 的圆的方程.
的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校因为寒假延期开学,根据教育部停课不停学的指示,该学校组织学生线上教学,高一年级在线上教学一个月后,为了了解线上教学的效果,在线上组织数学学科考试,随机抽取50名学生(满分150分,且抽取的学生成绩都在![]() 内)的成绩并制成频率分布直方图如图所示.
内)的成绩并制成频率分布直方图如图所示.
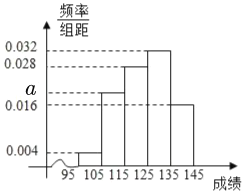
(1)根据频率分布直方图,估计这50名同学的数学平均成绩;(同一组中的数据以该组区间的中点值作代表)
(2)用分层抽样的方法从成绩在![]() 和
和![]() 的同学中抽取6名,再在抽取的这6名同学中任选2名,求这两名同学的数学成绩在同一组中的概率.
的同学中抽取6名,再在抽取的这6名同学中任选2名,求这两名同学的数学成绩在同一组中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2013年春节,有超过20万名广西、四川等省籍的外来务工人员选择驾驶摩托车沿321国道返乡过年,为保证他们的安全,交管部门在321国道沿线设立多个驾乘人员休息站,交警小李在某休息站连续5天对进站休息的驾驶人员每隔50辆摩托车,就进行省籍询问一次,询问结果如下图所示.

(Ⅰ)问交警小李对进站休息的驾驶人员的省籍询问采用的是什么抽样方法?
(Ⅱ)用分层抽样的方法对被询问了省籍的驾驶人员进行抽样,若广西籍的有5名,则四川籍的应抽取几名?
(Ⅲ)在上述抽出的驾驶人员中任取2名,求至少有一名驾驶人员是广西籍的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年9月,第22届鲁台经贸洽谈会在潍坊鲁台会展中心举行,在会展期间某展销商销售一种商品,根据市场调查,每件商品售价![]() (元)与销量
(元)与销量![]() (万件)之间的函数关系如图所示,又知供货价格与销量成反比,比例系数为20.(注:每件产品利润=售价-供货价格)
(万件)之间的函数关系如图所示,又知供货价格与销量成反比,比例系数为20.(注:每件产品利润=售价-供货价格)

(Ⅰ)求售价15元时的销量及此时的供货价格;
(Ⅱ)当销售价格为多少时总利润最大,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右顶点是双曲线
的左右顶点是双曲线![]() 的顶点,且椭圆
的顶点,且椭圆![]() 的上顶点到双曲线
的上顶点到双曲线![]() 的渐近线的距离为
的渐近线的距离为![]() 。
。
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 相交于
相交于![]() 两点,与
两点,与![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,学案导学模式已经成为教学中不可或缺的一部分,为了了解学案的合理使用是否对学生的期末复习有着重要的影响,我校随机抽取100名学生,对学习成绩和学案使用程度进行了调查,统计数据如表所示:

已知随机抽查这100名学生中的一名学生,抽到善于使用学案的学生概率是0.6.

参考公式:![]() ,其中
,其中 ![]() .
.
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法有多大的把握认为学生的学习成绩与对待学案的使用态度有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),且直线
为参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,以直角坐标系的原点为极点,以
两点,以直角坐标系的原点为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2) 已知点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com