
)已知|a|=4,|b|=3,(2a-3b)·(2a+b)=61.
(1)求a与b的夹角θ;
(2)求|a+b|和|a-b|;
 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中数学 来源: 题型:解答题
设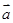 =(-1,1),
=(-1,1), =(x,3),
=(x,3), =(5,y),
=(5,y), =(8,6),且
=(8,6),且 ∥
∥ ,(4
,(4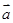 +
+ )⊥
)⊥ .
.
(1)求 和
和 ;
;
(2)求 在
在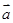 方向上的射影;
方向上的射影;
(3)求λ1和λ2,使 =λ1
=λ1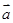 +λ2
+λ2 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知平面向量 ,
,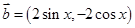 ,
,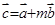 ,
, ,
,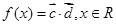 .
.
(1)当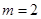 时,求
时,求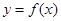 的取值范围;
的取值范围;
(2)若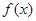 的最大值是
的最大值是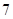 ,求实数
,求实数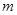 的值;
的值;
(3)(仅理科同学做,文科同学不做)若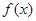 的最大值是
的最大值是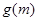 ,对任意的
,对任意的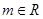 ,都有
,都有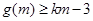 恒成立,求实数
恒成立,求实数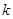 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com