
分析 ①当$\overrightarrow{a}$=$\overrightarrow{0}$时,$\overrightarrow{b}$∥$\overrightarrow{c}$不一定成立;
②利用向量平行的坐标表示,列出方程求出k的值;
③利用平面向量的几何意义,画出图形,即可得出正确的结论.
解答 解:对于①,当$\overrightarrow{a}$∥$\overrightarrow{b}$且$\overrightarrow{a}$∥$\overrightarrow{c}$,若$\overrightarrow{a}$=$\overrightarrow{0}$,则$\overrightarrow{b}$∥$\overrightarrow{c}$不一定成立,∴①错误;
对于②,当$\overrightarrow{a}$=(2,k),$\overrightarrow{b}$=(-2,6),且$\overrightarrow{a}$∥$\overrightarrow{b}$时,-2k-2×6=0,解得k=-6,∴②正确;
对于③,根据平面向量的几何意义,得;
非零向量$\overrightarrow{a}$和$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|时,以|$\overrightarrow{a}$|、|$\overrightarrow{b}$|、|$\overrightarrow{a}$-$\overrightarrow{b}$|为三边的三角形是等腰三角形,
如图所示,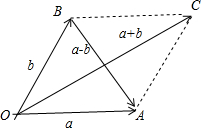
则$\overrightarrow{a}$与$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为30°,∴③正确.
综上,正确的命题是②③.
故答案为:②③.
点评 本题考查了平面向量的基本概念的应用问题,也考查了平面向量的几何意义的应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1+x2+x3有最小值,x1x2x3无最大值 | |
| B. | x1+x2+x3无最小值,x1x2x3有最大值 | |
| C. | x1+x2+x3有最小值,x1x2x3有最大值 | |
| D. | x1+x2+x3无最小值,x1x2x3无最大值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M⊆N | B. | M=N | C. | N⊆M | D. | M∩N=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 3或4 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com