
分析 利用条件计算S1,S2,S3,由此推测Sn的计算公式;利用归纳法进行证明,检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
解答 解:S1=$\frac{1}{3}$,S2=$\frac{2}{5}$,S3=$\frac{3}{7}$
猜想:Sn=$\frac{n}{2n+1}$.
①n=1时,S1成立;
②假设n=k时,猜想成立,即Sk=$\frac{k}{2k+1}$,
则n=k+1时,Sk+1=$\frac{k}{2k+1}$+$\frac{1}{(2k+1)(2k+3)}$=$\frac{k+1}{2(k+1)+1}$,
∴n=k+1时猜想也成立
根据①②可知猜想对任何n∈N*都成立
点评 本题考查归纳推理,用数学归纳法证明等式,证明故当n=k+1时,猜想也成立,是解题的难点和关键.


科目:高中数学 来源: 题型:选择题
| A. | k≤-3或-1≤k≤1或k≥3 | B. | 不存在这样的实数k | ||
| C. | -2<k<2 | D. | -3<k<-1或1<k<3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 60°或300° | C. | 30° | D. | 30°或330° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<2} | B. | {x|1≤x<2} | C. | {x|x>0} | D. | {x|x≥1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | (-∞,$\frac{1}{2}$) | C. | (-1,0)∪(0,$\frac{1}{2}$) | D. | (-∞,-1)∪(-1,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
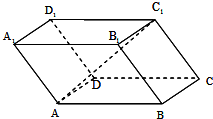 已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,侧棱AA1的长为2,∠A1AB=∠A1AD=120°.
已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,侧棱AA1的长为2,∠A1AB=∠A1AD=120°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com