
设函数f(x)=sin2ωx+2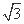 sin ωx·cos ωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
sin ωx·cos ωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(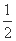 ,1).
,1).
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点( ,0),求函数f(x)的值域.
,0),求函数f(x)的值域.
科目:高中数学 来源: 题型:
已知抛物线y2=4x的焦点为F,过F的直线与该抛物线相交于A(x1,y1)、B(x2,y2)两点,则 +
+ 的最小值是( )
的最小值是( )
(A)4 (B)8 (C)12 (D)16
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,已知C点在圆O直径BE的延长线上,CA切圆O于A点,∠ACB的平分线CD交AE于点F,交AB于点D.

(1)求∠ADF的度数;
(2)若AB=AC,求AC∶BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,假设正确的是( )
(A)假设三个内角都不大于60度
(B)假设三个内角都大于60度
(C)假设三个内角至多有一个大于60度
(D)假设三个内角有两个大于60度
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=2sin(ωx+),x∈R,其中ω>0,-π<≤π.若f(x)的最小正周期为6π,且当x=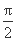 时,f(x)取得最大值,则( )
时,f(x)取得最大值,则( )
(A)f(x)在区间[-2π,0]上是增函数
(B)f(x)在区间[-3π,-π]上是增函数
(C)f(x)在区间[3π,5π]上是减函数
(D)f(x)在区间[4π,6π]上是减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=(2cos2x-1)sin 2x+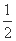 cos 4x.
cos 4x.
(1)求f(x)的最小正周期及最大值;
(2)若α∈(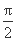 ,π),且f(α)=
,π),且f(α)=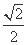 ,求α的值.
,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知双曲线E的中心为原点,F(3,0)是E的焦点,过F的直线l与E相交于A、B两点,且AB的中点为N(-12,-15),则E的方程为( )
(A)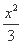 -
-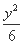 =1 (B)
=1 (B) 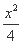 -
-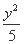 =1
=1
(C)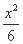 -
-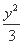 =1 (D)
=1 (D)  -
-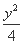 =1
=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com