
分析 (1)结合对勾函数和一次函数的图象和性质,可得结论;
(2)分类讨论满足y≥1的x范围,综合讨论结果,可得答案;
(3)根据已知求出函数的解析式,分析其单调性后,可得函数的最值.
解答 解:(1)函数在[0,2]上单调递增,在(2,4]上单调递减;…(2分)
(2)解$\left\{\begin{array}{l}-\frac{16}{x+2}-x+8≥1\\ 0≤x≤2\end{array}\right.$得:$\frac{5-\sqrt{17}}{2}≤x≤2$--------(4分)
解$\left\{\begin{array}{l}4-x≥1\\ 2<x≤4\end{array}\right.$得:2<x≤3…(5分)
综上可得$\frac{5-\sqrt{17}}{2}≤x≤3$…(6分)
即若1个单位的固体碱只投放一次,则能够维持有效抑制作用的时间为$3-\frac{5-\sqrt{17}}{2}$=$\frac{1+\sqrt{17}}{2}$…(7分)
(3)由(1)知,当0≤x≤2时,y=$-\frac{16}{x+2}-x+8$单调递增
当2<x≤4时,y=4-x单调递减
所以当河中的碱浓度开始下降时,即刻第二次投放1个单位的固体碱,
即2<x≤4时,
y=4-x+$[-\frac{16}{(x-2)+2}-(x-2)+8]$=14-(2x+$\frac{16}{x}$)…(10分)
记$f(x)=2x+\frac{16}{x}$,
下面用单调函数的定义证明f(x)在$(2,2\sqrt{2})$上单调递减,$(2\sqrt{2},4)$上单调递增.
对任意x1,x2满足,$2<{x_1}<{x_2}<2\sqrt{2}$,
$\begin{array}{l}f({x_1})-f({x_1})=(2{x_1}+\frac{16}{x_1})-(2{x_2}+\frac{16}{x_2})\\=({x_1}-{x_2})\frac{{2{x_1}{x_2}-16}}{{{x_1}{x_2}}}>0\end{array}$
∴f(x1)>f(x2),
所以,f(x)在$(2,2\sqrt{2})$上单调递减,同理可证,f(x)在$(2\sqrt{2},4)$上单调递增.
故当且仅当$2x=\frac{16}{x}$,即x=2$\sqrt{2}$时,
$f{(x)_{min}}=f(2\sqrt{2})=8\sqrt{2}$,
所以y有最大值14-8$\sqrt{2}$.…(12分)
点评 本题考查的知识点是分段函数的应用,基本不等式,难度中档.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $|{\begin{array}{l}0\\ 1\end{array}}|$ | B. | $|{\begin{array}{l}1\\ 0\end{array}}|$ | C. | $|{\begin{array}{l}0\\ 0\end{array}}|$ | D. | $|{\begin{array}{l}1\\{-1}\end{array}}|$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
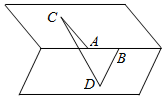 如图,已知在一个二面角的棱上有两个点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,AB=4cm,AC=6cm,BD=8cm,CD=2$\sqrt{17}$cm,则这个二面角的度数为60°.
如图,已知在一个二面角的棱上有两个点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,AB=4cm,AC=6cm,BD=8cm,CD=2$\sqrt{17}$cm,则这个二面角的度数为60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com