
分析 (1)首先通过恒等变换函数变形成正弦型函数,进一步求出单调区间;
(2)先求出sin(x+$\frac{π}{3}$)=$\frac{1}{6}$,再根据二倍角公式即可求出答案.
解答 解:(1)函数f(x)=2cos(x+$\frac{π}{6}$)+2sinx=2($\frac{\sqrt{3}}{2}$cosx-$\frac{1}{2}$sinx)+2sinx=2($\frac{\sqrt{3}}{2}$cosx+$\frac{1}{2}$sinx)=2sin(x+$\frac{π}{3}$),
由2kπ+$\frac{π}{2}$≤x+$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,k∈Z,
得2kπ+$\frac{π}{6}$≤x≤2kπ+$\frac{7π}{6}$,k∈Z,
∴函数f(x)的单调递减区间为[2kπ+$\frac{π}{6}$,2kπ+$\frac{7π}{6}$],k∈Z;
(2)∵f(x)=$\frac{1}{3}$,
∴2sin(x+$\frac{π}{3}$)=$\frac{1}{3}$,
∴sin(x+$\frac{π}{3}$)=$\frac{1}{6}$,
∴cos(2x+$\frac{2π}{3}$)=1-2sin2(x+$\frac{π}{3}$)=1-$\frac{1}{18}$=$\frac{17}{18}$.
点评 本题考查三角函数关系式的恒等变换,二倍角公式,正弦型函数的单调区间的求法.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{3}$ | C. | -3 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | (2,+∞) | C. | (-1,2] | D. | [-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,1} | B. | {-1,3} | C. | {3,1,-1} | D. | {1,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
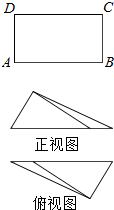 如图,在矩形ABCD中,$AB=\sqrt{3}$,BC=1,沿AC将矩形ABCD折叠,连接BD,所得三棱锥D-ABC的正视图和俯视图如图所示,则三棱锥D-ABC的侧视图的面积为( )
如图,在矩形ABCD中,$AB=\sqrt{3}$,BC=1,沿AC将矩形ABCD折叠,连接BD,所得三棱锥D-ABC的正视图和俯视图如图所示,则三棱锥D-ABC的侧视图的面积为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
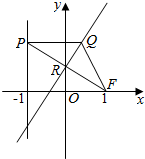 在平面直角坐标系xoy中,设点F(1,0),直线l:x=-1,点P在直线l上移动,R是线段PF与y轴的交点,RQ⊥FP,PQ⊥l.
在平面直角坐标系xoy中,设点F(1,0),直线l:x=-1,点P在直线l上移动,R是线段PF与y轴的交点,RQ⊥FP,PQ⊥l.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
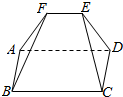 如图,在五面体ABCDEF中,四边形ABCD为正方形,BA⊥平面ADEF,DE⊥AF,AF=1,AD=2$\sqrt{2}$.
如图,在五面体ABCDEF中,四边形ABCD为正方形,BA⊥平面ADEF,DE⊥AF,AF=1,AD=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,4) | B. | [-2,4] | C. | (-∞,1]∪(2,4) | D. | (-∞,1)∪(2,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com