
分析 (Ⅰ)当a=3时,根据函数f(x)=|x+3|+|x-2|的意义,求得不等式f(x)≥7的解集.
(Ⅱ)由题意可得,当x∈[0,2]时,|x+a|≤|x-4|-|x-2|恒成立,等价于-2-a≤x≤2-a,根据-2-a≤0,2-a≥2,求得a的范围.
解答 解:(Ⅰ)当a=3时,函数f(x)=|x+3|+|x-2|表示数轴上的x对应点到-3、2对应点的距离之和,
而-4和3对应点到-3、2对应点的距离之和正好等于7,
故不等式f(x)≥7的解集为{x|x≤-4 或x≥3}.
(Ⅱ)若f(x)≤|x-4|的解集包含[0,2],即当x∈[0,2]时,|x+a|+|x-2|≤|x-4|恒成立,
即|x+a|≤|x-4|-|x-2|恒成立,
等价于-2-a≤x≤2-a.
由题意可得,-2-a≤0,2-a≥2,求得-2≤a≤0.
点评 本题主要考查绝对值的意义,绝对值不等式的解法,函数的恒成立问题,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|x<-1} | B. | {x|x>1} | C. | {x|x<-1或x>1} | D. | {x|-1<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 工人编号 年龄 | 工人编号 年龄 | 工人编号 年龄 | 工人编号 年龄 |
| 1 40 2 44 3 40 4 41 5 33 6 40 7 45 8 42 9 43 | 10 36 11 31 12 38 13 39 14 43 15 45 16 39 17 38 18 36 | 19 27 20 43 21 41 22 37 23 34 24 42 25 37 26 44 27 42 | 28 34 29 39 30 43 31 38 32 42 33 53 34 37 35 49 36 39 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
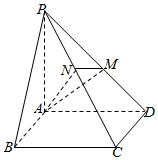 如图,四棱锥P-ABCD的底面为正方形,PA⊥平面ABCD,PA=AD,点M、N分别在棱PD、PC上,且PC⊥平面AMN.
如图,四棱锥P-ABCD的底面为正方形,PA⊥平面ABCD,PA=AD,点M、N分别在棱PD、PC上,且PC⊥平面AMN.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com