
【题目】已知函数![]() ,
, ![]() 的图象在
的图象在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求函数![]() 的单调区间与极值;
的单调区间与极值;
(2)若存在实数![]() ,使得
,使得![]() 成立,求整数
成立,求整数![]() 的最小值.
的最小值.
【答案】(1) 函数f(x)的单调递减区间为(-∞,0);单调递增区间为(0,+∞),所以函数f(x)在x=0处取得极小值f(0)=2;(2) k的最小值为0.
【解析】试题分析:⑴求出函数![]() 的导数,求得切线的切点,
的导数,求得切线的切点,
⑵要满足![]() ,分类含参量得
,分类含参量得![]()
构造![]() ,求得
,求得![]() 的最小值即可
的最小值即可
解析:(Ⅰ)f′(x)=2ex+6x-2,
因为f′(0)=a,所以a=0,
易得切点(0,2),所以b=-1.
易知函数f′(x)在R上单调递增,且f′(0)=0.
则当x<0时,f′(x)<0;当x>0时,f′(x)>0.
所以函数f(x)的单调递减区间为(-∞,0);单调递增区间为(0,+∞).
所以函数f(x)在x=0处取得极小值f(0)=2.
(Ⅱ)f(x)-2x2-3x-2-2k≤0![]() ex+
ex+![]() x2-
x2-![]() x-1-k≤0
x-1-k≤0![]() k≥ex+
k≥ex+![]() x2-
x2-![]() x-1, (*)
x-1, (*)
令h(x)=ex+![]() x2-
x2-![]() x-1,
x-1,
若存在实数x,使得不等式(*)成立,则k≥h(x)min,
h′(x)=ex+x-![]() ,易知h′(x)在R上单调递增,
,易知h′(x)在R上单调递增,
又h′(0)=-![]() <0,h′(1)=e-
<0,h′(1)=e-![]() >0,h′
>0,h′![]() =e
=e![]() -2<0,h′
-2<0,h′![]() =e
=e![]() -
-![]() >2.56
>2.56![]() -
-![]() =1.6
=1.6![]() -
-![]() =
=![]() -
-![]() >2-
>2-![]() =
=![]() >0,
>0,
![]()
![]()
所以存在唯一的x0∈![]() ,使得h′(x0)=0,
,使得h′(x0)=0,
且当x∈(-∞,x0)时,h′(x)<0;当x∈(x0,+∞)时,h′(x)>0.
所以h(x)在(-∞,x0)上单调递减,在(x0,+∞)上单调递增,
h(x)min=h(x0)=ex0+![]() x20-
x20-![]() x0-1,
x0-1,
又h′(x0)=0,即ex0+x0-![]() =0,
=0,
所以ex0=![]() -x0.
-x0.
所以![]()
![]()
因为x0∈![]() ,
,
所以h(x0)∈![]() ,
,
则k≥h(x0),又k∈Z.
所以k的最小值为0.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为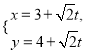 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,并使得它与直角坐标系
轴的正半轴为极轴建立极坐标系,并使得它与直角坐标系![]() 有相同的长度单位,曲线
有相同的长度单位,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() 点的坐标为
点的坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现在的人基本每天都离不开手机,许多人手机一旦不在身边就不舒服,几乎达到手机二十四小时不离身,这类人群被称为“手机控”,这一群体在大学生中比较突出.为了调查大学生每天使用手机的时间,某调查公司针对某高校男生、女生各25名学生进行了调查,其中每天使用手机时间超过8小时的被称为:“手机控”,否则被称为“非手机控”.调查结果如下:
手机控 | 非手机控 | 合计 | |
女生 | 5 | ||
男生 | 10 | ||
合计 | 50 |
(1)将上面的列联表补充完整,再判断是否有99.5%的把握认为“手机控”与性别有关,说明你的理由;
(2)现从被调查的男生中按分层抽样的方法选出5人,再从这5人中随机选取3人参加座谈会,记这3人中“手机控”的人数为![]() ,试求
,试求![]() 的分布列与数学期望.
的分布列与数学期望.
参考公式: 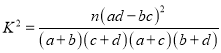 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() ,
, ![]() 为椭圆的上顶点,
为椭圆的上顶点, ![]() 为等边三角形,且其面积为
为等边三角形,且其面积为![]() ,
, ![]() 为椭圆的右顶点.
为椭圆的右顶点.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点(
两点(![]() 不是左、右顶点),且满足
不是左、右顶点),且满足![]() ,试问:直线
,试问:直线![]() 是否过定点?若过定点,求出该定点的坐标,否则说明理由.
是否过定点?若过定点,求出该定点的坐标,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,且过点
的焦点重合,且过点![]() .过点
.过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() 为椭圆的左顶点.
为椭圆的左顶点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)求![]() 面积的最大值,并求此时直线
面积的最大值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某技术公司开发的某种产品中随机抽取200件,测量这些产品的一项质量指标值(记为![]() ),由测量结果得到如下频率分布直方图:
),由测量结果得到如下频率分布直方图:
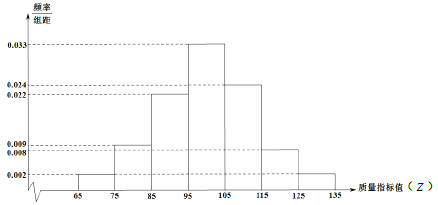
公司规定:当![]() 时,产品为正品;当
时,产品为正品;当![]() 时,产品为次品,公司每生产一件这种产品,若是正品,则盈利90元;若是次品,则亏损30元,记
时,产品为次品,公司每生产一件这种产品,若是正品,则盈利90元;若是次品,则亏损30元,记![]() 的分布列和数学期望;
的分布列和数学期望;
由频率分布直方图可以认为,![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() (同一组中的数据用该区间的中点值作代表)
(同一组中的数据用该区间的中点值作代表)
①利用该正态分布,求![]() ;
;
②某客户从该公司购买了500件这种产品,记![]() 表示这500件产品中该项质量指标值位于区间
表示这500件产品中该项质量指标值位于区间![]() 的产品件数,利用①的结果,求
的产品件数,利用①的结果,求![]() .
.
附:![]() ,
,
若![]() ,则
,则![]() ,
,
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com